Newton-Leibniz formula
The formula expressing the value of a definite integral of a given function 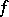 over an interval as the difference of the values at the end points of the interval of any primitive (cf. Integral calculus)
over an interval as the difference of the values at the end points of the interval of any primitive (cf. Integral calculus) 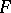 of the function
of the function 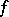 :
:
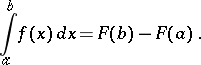 | (*) |
It is named after I. Newton and G. Leibniz, who both knew the rule expressed by (*), although it was published later.
If 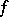 is Lebesgue integrable over
is Lebesgue integrable over 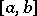 and
and 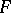 is defined by
is defined by
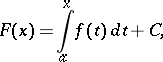 |
where 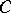 is a constant, then
is a constant, then 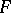 is absolutely continuous,
is absolutely continuous, 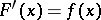 almost-everywhere on
almost-everywhere on 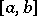 (everywhere if
(everywhere if 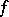 is continuous on
is continuous on  ) and (*) is valid.
) and (*) is valid.
A generalization of the Newton–Leibniz formula is the Stokes formula for orientable manifolds with a boundary.
Comments
The theorem expressed by the Newton–Leibniz formula is called the fundamental theorem of calculus, cf. e.g. [a1].
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 318ff |
| [a2] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 165ff |
Newton-Leibniz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Newton-Leibniz_formula&oldid=17006