Nevanlinna-Pick interpolation
Nevanlinna–Pick interpolation problem
The data for the classical Nevanlinna–Pick interpolation problem [a13], [a15] consist of  distinct points
distinct points  in the open unit disc
in the open unit disc  and complex numbers
and complex numbers  . Given these data, the problem is to find (if possible) a function
. Given these data, the problem is to find (if possible) a function  , the Hardy space of all bounded analytic functions on
, the Hardy space of all bounded analytic functions on  (cf. also Hardy classes), such that:
(cf. also Hardy classes), such that:
a)  for
for  ;
;
b) 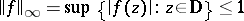 . Instead of condition b) one may require the
. Instead of condition b) one may require the 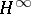 norm of the interpolant
norm of the interpolant  to be strictly less than one, and in the latter case one calls the problem suboptimal. The problem may also be considered for infinite collections of points ([a14]).
to be strictly less than one, and in the latter case one calls the problem suboptimal. The problem may also be considered for infinite collections of points ([a14]).
The Nevanlinna–Pick interpolation problem is solvable if and only if the associated Pick matrix
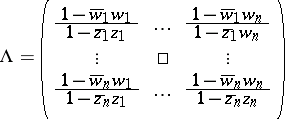 |
is positive semi-definite, and its solution is unique if and only if, in addition, 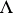 is singular. For the suboptimal version of the problem to be solvable it is necessary and sufficient that the Pick matrix
is singular. For the suboptimal version of the problem to be solvable it is necessary and sufficient that the Pick matrix 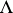 be positive definite, and in this case there is a rational
be positive definite, and in this case there is a rational 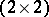 -matrix function
-matrix function 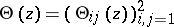 such that the infinitely many solutions
such that the infinitely many solutions  of the problem are described by
of the problem are described by
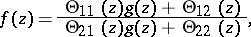 |
where the free parameter 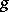 is an arbitrary
is an arbitrary 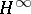 -function with
-function with 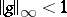 . Moreover, for
. Moreover, for  one may take (see [a2], Sect. 18.1) the matrix function
one may take (see [a2], Sect. 18.1) the matrix function
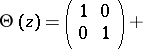 |
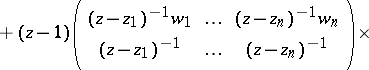 |
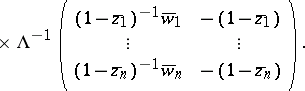 |
Matrix- and operator-valued versions of the Nevanlinna–Pick problem, including one-sided and two-sided tangential variants, have also been introduced, and many different approaches have been developed to treat the problem and its various generalizations. For the history of the subject, see [a2], [a7], [a8], [a16], [a12].
The Nevanlinna–Pick interpolation theorems and their matrix generalizations have proved to be very useful in solving engineering problems, in particular, in circuit theory [a4] and for control theory problems involving an  -criterion (see [a10] and [a6], Chapt. 9). This development led to a new field of research, in which the emphasis is on interpolants that are rational matrix functions and on the search for explicit formulas and efficient algorithms for the construction of interpolants in a form which is suitable for engineering applications (see [a2], Part VI, and [a18]).
-criterion (see [a10] and [a6], Chapt. 9). This development led to a new field of research, in which the emphasis is on interpolants that are rational matrix functions and on the search for explicit formulas and efficient algorithms for the construction of interpolants in a form which is suitable for engineering applications (see [a2], Part VI, and [a18]).
The Nevanlinna–Pick problem also has a non-stationary version, in which the role of analytic functions is taken over by lower-triangular operators and points in the open unit disc are replaced by weighted shifts with spectral radius strictly less than one. To give an example, let  and
and  be two bounded sequences of complex numbers, and assume that
be two bounded sequences of complex numbers, and assume that
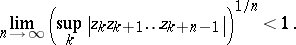 |
The non-stationary Nevanlinna–Pick interpolation problem associated with these data is to find a lower-triangular operator
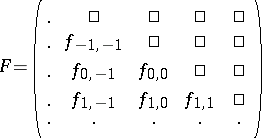 |
with operator norm 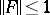 such that
such that
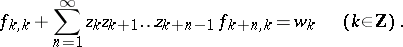 |
Several methods to treat such non-stationary interpolation problems have been developed (see [a11], [a5] and [a17]); the main results for the stationary case carry over to the non-stationary case (cf. [a9]).
Nevanlinna–Pick interpolation problems have also been solved for analytic functions on a half-plane. A non-stationary analogue of the latter may be found in [a1]. Generalizations of the Nevanlinna–Pick interpolation theory have also been developed for functions of several variables (see [a16], notes to Chapt. 2) and in a non-linear setting [a3].
References
| [a1] | J.A. Ball, I. Gohberg, M.A. Kaashoek, "Nevanlinna–Pick interpolation for time-varying input-output maps: The continuous time case" I. Gohberg (ed.) , Time-Variant Systems and Interpolation , Operator Theory: Advances and Applications , 56 , Birkhäuser (1992) pp. 52–89 |
| [a2] | J.A. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , Operator Theory: Advances and Applications , 45 , Birkhäuser (1990) |
| [a3] | J. Ball, J.W. Helton, "Shift invariant manifolds and nonlinear analytic function theory" Integral Eq. Operator Th. , 11 (1988) pp. 615–725 |
| [a4] | Ph. Delsarte, Y. Genin, Y. Kamp, "On the role of the Nevanlinna–Pick problem in circuit and system theory" Internat. J. Circuit Th. Appl. , 9 (1981) pp. 177–187 |
| [a5] | P. Dewilde, M.A. Kaashoek, M. (eds.) Verhaegen, "Challenges of a generalized system theory" KNWA Verhandelingen, Afd. Natuurkunde, Eerste reeks , 40 (1993) |
| [a6] | J.C. Doyle, B.A. Francis, A.R. Tannenbaum, "Feedback control theory" , Macmillan (1992) |
| [a7] | H. Dym, " contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) |
| [a8] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a9] | C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" Integral Eq. Operator Th. , 26 (1996) pp. 371–403 |
| [a10] | B.A. Francis, "A course in  control theory" , Springer (1987) control theory" , Springer (1987) |
| [a11] | "Time-variant systems and interpolation" I. Gohberg (ed.) , Operator Theory: Advances and Applications , 56 , Birkhäuser (1992) |
| [a12] | "Matrix and operator valued functions: The Vladimir Petrovich Potapov Memorial Volume" I. Gohberg (ed.) L.A. Sakhnovich (ed.) , Operator Theory: Advances and Applications , 72 , Birkhäuser (1994) |
| [a13] | R. Nevanlinna, "Über beschränkte analytische Funktionen die in gegebene Punkten vorgeschriebene Werte annehmen" Ann. Acad. Sci. Fenn. Ser. A , 13 : 1 (1919) pp. 1–71 |
| [a14] | R. Nevanlinna, "Über beschränkte analytische Funktionen" Ann. Acad. Sci. Fenn. Ser. A , 32 : 7 (1929) pp. 1–75 |
| [a15] | G. Pick, "Über beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" Math. Ann. , 77 (1916) pp. 7–23 |
| [a16] | M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Mathematical Monographs , Oxford Univ. Press (1985) |
| [a17] | A.H. Sayed, T. Constantinescu, T. Kailath, "Lattice structures of time-variant interpolation problems" , Proc. 1-st IEEE Conf. Decision and Control, (Tuscon, AZ, Dec.1992) (1992) |
| [a18] | A.H. Sayed, T. Kailath, H. Lev-Ari, T. Constantinescu, "Recursive solutions of rational interpolation problems via fast matrix factorization" Integral Eq. Operator Th. , 20 (1994) pp. 84–118 |
Nevanlinna-Pick interpolation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna-Pick_interpolation&oldid=11418