Neumann eigenvalue

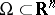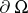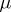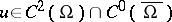Consider a bounded domain with a piecewise smooth boundary . A number is a Neumann eigenvalue of if there exists a function (a Neumann eigenfunction) satisfying the following Neumann boundary value problem (cf. also Neumann boundary conditions):

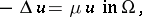(a1)

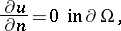(a2)

where 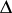is the Laplace operator (i.e., 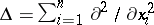). For more general definitions, see [a8]. Neumann eigenvalues (with ) appear naturally when considering the vibrations of a free membrane (cf. also Natural frequencies). In fact, for 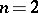the non-zero Neumann eigenvalues are proportional to the square of the eigenfrequencies of the membrane with free boundary. Provided is bounded and the boundary 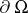is sufficiently regular, the Neumann Laplacian has a discrete spectrum of infinitely many non-negative eigenvalues with no finite accumulation point:

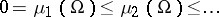(a3)

( as 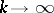). The Neumann eigenvalues are characterized by the max-min principle [a3]:

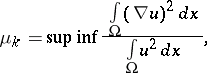(a4)

where the 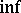is taken over all 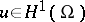orthogonal to 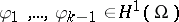, and the 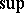is taken over all the choices of 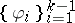. For simply-connected domains the first eigenfunction 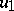, corresponding to the eigenvalue 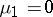is constant throughout the domain. All the other eigenvalues are positive. While Dirichlet eigenvalues satisfy stringent constraints (e.g., 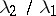cannot exceed 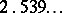for any bounded domain in 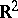, [a1]; see also Dirichlet eigenvalue), no such constraints exist for Neumann eigenvalues, other than the fact that they are non-negative. In fact, given any finite sequence 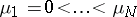, there is an open, bounded, smooth, simply-connected domain of 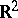having this sequence as the first 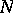Neumann eigenvalues of the Laplacian on that domain [a2]. Though it is obvious from the variational characterization of both Dirichlet and Neumann eigenvalues (see (a4)) that 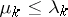, L. Friedlander [a4] proved the stronger result

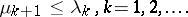(a5)

How far the first non-trivial Neumann eigenvalue is from zero for a convex domain in 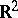is given through the optimal inequality [a7]

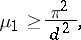(a6)

where 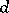is the diameter of the domain. There are many more isoperimetric inequalities for Neumann eigenvalues (see Rayleigh–Faber–Krahn inequality).

For large values of 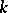, H. Weyl proved [a9]

(a7)

where 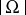and are, respectively, the volumes of and of the unit ball in .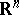

For any plane-covering domain (i.e., a domain that can be used to tile the plane without gaps, nor overlaps, allowing rotations, translations and reflections of itself), G. Pólya [a6] proved that

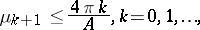(a8)

and conjectured the same bound for any bounded domain in 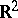. This is equivalent to saying that the Weyl asymptotics of 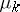is an upper bound for 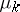. The analogous conjecture in dimension is

(a9)

The most significant result towards the proof of Pólya's conjecture for Neumann eigenvalues is the result by P. Kröger [a5]:

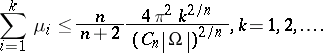A proof of Pólya's conjecture for both Dirichlet and Neumann eigenvalues would imply Friedlander's result (a5).

References

[a1]	M.S. Ashbaugh, R.D. Benguria, "A sharp bound for the ratio of the first two eigenvalues of Dirichlet Laplacians and extensions" Ann. of Math. , 135 (1992) pp. 601–628
[a2]	Y. Colin de Vérdiere, "Construction de laplaciens dont une partie finie du spectre est donnée" Ann. Sci. École Norm. Sup. , 20 : 4 (1987) pp. 599–615
[a3]	R. Courant, D. Hilbert, "Methoden der mathematischen Physik" , I , Springer (1931) (English transl.: Methods of Mathematical Physics, vol. I., Interscience, 1953)
[a4]	L. Friedlander, "Some inequalities between Dirichlet and Neumann eigenvalues" Arch. Rational Mech. Anal. , 116 (1991) pp. 153–160
[a5]	P. Kröger, "Upper bounds for the Neumann eigenvalues on a bounded domain in Euclidean Space" J. Funct. Anal. , 106 (1992) pp. 353–357
[a6]	G. Polya, "On the eigenvalues of vibrating membranes" Proc. London Math. Soc. , 11 : 3 (1961) pp. 419–433
[a7]	L.E. Payne, H.F. Weinberger, "An optimal Poincaré inequality for convex domains" Arch. Rational Mech. Anal. , 5 (1960) pp. 286–292
[a8]	M. Reed, B. Simon, "Methods of modern mathematical physics IV: Analysis of operators" , Acad. Press (1978)
[a9]	H. Weyl, "Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen" Math. Ann. , 71 (1911) pp. 441–479