Net (of sets in a topological space)
network (of sets in a topological space)
A family  of subsets of a topological space
of subsets of a topological space  such that for each
such that for each  and each neighbourhood
and each neighbourhood  of
of  there is an element
there is an element  of
of  such that
such that  .
.
The family of all one-point subsets of a space and every base of a space are networks. The difference between a network and a base is that the elements of a network need not be open sets. Networks appear under continuous mappings: If  is a continuous mapping of a topological space
is a continuous mapping of a topological space 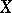 onto a topological space
onto a topological space 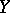 and
and  is a base of
is a base of 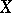 , then the images of the elements of
, then the images of the elements of 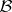 under
under 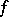 form a network
form a network 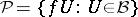 in
in 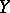 . Further, if
. Further, if 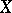 is covered by a family
is covered by a family 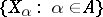 of subspaces, then, taking for each
of subspaces, then, taking for each  any base
any base 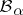 of
of  and amalgamating these bases, a network
and amalgamating these bases, a network  in
in  is obtained. Spaces with a countable network are characterized as images of separable metric spaces under continuous mappings.
is obtained. Spaces with a countable network are characterized as images of separable metric spaces under continuous mappings.
The minimum cardinality of a network of a space 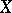 is called the network weight, or net weight, of
is called the network weight, or net weight, of 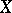 and is denoted by
and is denoted by 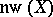 . The net weight of a space never exceeds its weight (cf. Weight of a topological space), but, as is shown by the example of a countable space without a countable base, the net weight can differ from the weight. For compact Hausdorff spaces the net weight coincides with the weight. This result extends to locally compact spaces, Čech-complete spaces and feathered spaces (cf. Feathered space). Hence, in particular, it follows that weight does not increase under surjective mappings of such spaces. Another corollary: If a feathered space
. The net weight of a space never exceeds its weight (cf. Weight of a topological space), but, as is shown by the example of a countable space without a countable base, the net weight can differ from the weight. For compact Hausdorff spaces the net weight coincides with the weight. This result extends to locally compact spaces, Čech-complete spaces and feathered spaces (cf. Feathered space). Hence, in particular, it follows that weight does not increase under surjective mappings of such spaces. Another corollary: If a feathered space  (in particular, a Hausdorff compactum) is given as the union of a family of cardinality
(in particular, a Hausdorff compactum) is given as the union of a family of cardinality 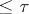 of subspaces, the weight of each of which does not exceed
of subspaces, the weight of each of which does not exceed  , supposed infinite, then the weight of
, supposed infinite, then the weight of 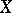 does not exceed
does not exceed  .
.
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [2] | A.V. Arkhangel'skii, "An addition theorem for weights of sets lying in bicompacta" Dokl. Akad. Nauk SSSR , 126 : 2 (1959) pp. 239–241 (In Russian) |
Comments
Most English-language texts (cf. e.g. [a4]) use network for the concept called "net" above. This is because the term "net" also has a second, totally different, meaning in general topology.
A net in a set (topological space) 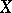 is an indexed set
is an indexed set  of points of
of points of 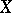 , where
, where  is a directed set. In Russian this is called a generalized sequence.
is a directed set. In Russian this is called a generalized sequence.
One can build a theory of convergence for nets: Moore–Smith convergence (cf. Moore space).
References
| [a1] | R. Engelking, "General topology" , PWN (1977) (Translated from Polish) (Revised and extended version of [3] above) |
| [a2] | J.L. Kelley, "Convergence in topology" Duke Math. J. , 17 (1950) pp. 277–283 |
| [a3] | E.H. Moore, H.L. Smith, "A general theory of limits" Amer. J. Math. , 44 (1922) pp. 102–121 |
| [a4] | J.-I. Nagata, "Modern general topology" , North-Holland (1985) |
Net (of sets in a topological space). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Net_(of_sets_in_a_topological_space)&oldid=17332