Nekrasov integral equation
From Encyclopedia of Mathematics
A non-linear integral equation of the form
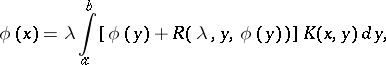 | (*) |
where 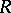 and
and 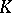 are known functions,
are known functions, 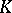 being symmetric,
being symmetric, 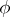 is the unknown function, and
is the unknown function, and 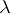 is a numerical parameter. Integral equations of this type were obtained by A.I. Nekrasov (see [1]) in the solution of problems arising in the theory of waves on the surface of a fluid. Under certain conditions Nekrasov has constructed a solution of (*) in the form of a series in powers of a small parameter; its convergence has been proved by the method of majorants.
is a numerical parameter. Integral equations of this type were obtained by A.I. Nekrasov (see [1]) in the solution of problems arising in the theory of waves on the surface of a fluid. Under certain conditions Nekrasov has constructed a solution of (*) in the form of a series in powers of a small parameter; its convergence has been proved by the method of majorants.
Sometimes an equation of the type (*) is called a Hammerstein equation, although Nekrasov [2] published his investigations before A. Hammerstein [3].
References
| [1] | A.I. Nekrasov, "Collected works" , 1 , Moscow (1961) (In Russian) |
| [2] | A.I. Nekrasov, Izv. Ivanovo-Vozn. Politekhn. Inst. , 6 (1922) pp. 155–171 |
| [3] | A. Hammerstein, "Nichtlineare Integralgleichungen nebst Anwendungen" Acta Math. , 54 (1930) pp. 117–176 |
Comments
References
| [a1] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
How to Cite This Entry:
Nekrasov integral equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nekrasov_integral_equation&oldid=17945
Nekrasov integral equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nekrasov_integral_equation&oldid=17945
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article