Negative vector bundle
A holomorphic vector bundle (cf. also Vector bundle, analytic)  over a complex space
over a complex space  that possesses a Hermitian metric
that possesses a Hermitian metric  such that the function
such that the function  on
on  is strictly pseudo-convex outside the zero section (this is denoted by
is strictly pseudo-convex outside the zero section (this is denoted by  ). The vector bundle
). The vector bundle  is negative if and only if the dual vector bundle
is negative if and only if the dual vector bundle  (see Positive vector bundle). If
(see Positive vector bundle). If  is a manifold, then the condition of being negative can be expressed in terms of the curvature of the metric
is a manifold, then the condition of being negative can be expressed in terms of the curvature of the metric 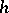 . Any subbundle of a negative vector bundle is negative. A vector bundle
. Any subbundle of a negative vector bundle is negative. A vector bundle  over a complex manifold is said to be negative in the sense of Nakano if
over a complex manifold is said to be negative in the sense of Nakano if 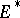 is positive in the sense of Nakano. A holomorphic vector bundle
is positive in the sense of Nakano. A holomorphic vector bundle 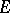 over a compact complex space
over a compact complex space 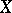 is said to be weakly negative if its zero section possesses a strictly pseudo-convex neighbourhood in
is said to be weakly negative if its zero section possesses a strictly pseudo-convex neighbourhood in 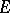 , i.e. if
, i.e. if 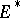 is weakly positive. Every negative vector bundle over
is weakly positive. Every negative vector bundle over 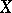 is weakly negative. Negative and weakly negative linear spaces over a space
is weakly negative. Negative and weakly negative linear spaces over a space  are also defined in this way.
are also defined in this way.
For references see Positive vector bundle.
Negative vector bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_vector_bundle&oldid=15576