Near-ring
One of the generalizations of the concept of an associative ring (cf. Associative rings and algebras). A near-ring is a ringoid over a group, i.e. a universal algebra in which an associative multiplication and addition exist; a near-ring is a (not necessarily Abelian) group with respect to addition, and the right distributive property
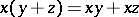 |
must hold too. A near-ring is also an example of a multi-operator group.
Examples of near-rings are the set 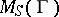 of all mappings of a group
of all mappings of a group 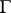 into itself which commute with the action of a given semi-group
into itself which commute with the action of a given semi-group 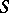 of endomorphisms of
of endomorphisms of 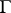 . The group operations in
. The group operations in 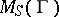 are defined pointwise and multiplication in
are defined pointwise and multiplication in 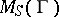 is composition of mappings. A near-ring
is composition of mappings. A near-ring 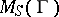 is an analogue of a ring of matrices. The notions of a sub-near-ring, of an ideal and of a right module over a near-ring are introduced in the usual manner.
is an analogue of a ring of matrices. The notions of a sub-near-ring, of an ideal and of a right module over a near-ring are introduced in the usual manner.
Let 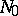 (
(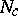 ) be the variety of near-rings defined by the identity
) be the variety of near-rings defined by the identity 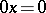 (
(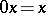 ). Every near-ring
). Every near-ring 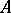 can be decomposed into the sum
can be decomposed into the sum 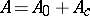 of sub-near-rings, where
of sub-near-rings, where  ,
, 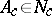 and
and 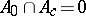 . A cyclic right
. A cyclic right 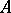 -module
-module 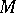 is called primitive of type
is called primitive of type  if
if  is simple; primitive of type 1 if either
is simple; primitive of type 1 if either 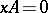 or
or 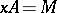 for any
for any 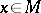 ; and primitive of type 2 if
; and primitive of type 2 if  is a simple
is a simple  -module. A near-ring
-module. A near-ring 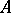 is called primitive of type
is called primitive of type  (
(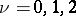 ) if there is a faithful simple
) if there is a faithful simple 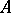 -module
-module 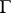 of type
of type  . In this case there is a dense imbedding of
. In this case there is a dense imbedding of 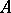 into
into 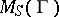 for some semi-group
for some semi-group 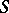 of endomorphisms of
of endomorphisms of 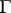 . For
. For  -primitive near-rings
-primitive near-rings 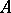 with an identity element and with the minimum condition for right ideals in
with an identity element and with the minimum condition for right ideals in 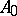 , the equality
, the equality 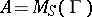 holds (an analogue of the Wedderburn–Artin theorem). For every
holds (an analogue of the Wedderburn–Artin theorem). For every 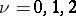 , the Jacobson radical
, the Jacobson radical 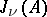 of type
of type  can be introduced as the intersection of the annihilators of
can be introduced as the intersection of the annihilators of  -primitive
-primitive  -modules. The radical
-modules. The radical  is defined as the intersection of the maximal right module ideals. All four radicals are different, and
is defined as the intersection of the maximal right module ideals. All four radicals are different, and
 |
It turns out that these radicals posses many properties of the Jacobson radical of an associative ring (cf. [4]).
For near-rings an analogue of Ore's theorem on near-rings of fractions [4] holds.
A distributively-generated near-ring is a near-ring whose additive group is generated by elements  such that
such that
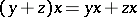 |
for all 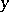 and
and  in the near-ring. All distributively-generated near-rings generate the variety
in the near-ring. All distributively-generated near-rings generate the variety 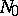 . For finite distributively-generated near-rings the notions of 1- and
. For finite distributively-generated near-rings the notions of 1- and  -primitivity coincide;
-primitivity coincide; 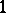 -primitive distributively-generated near-rings have the form
-primitive distributively-generated near-rings have the form 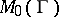 for some group
for some group 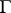 . In a distributively-generated near-ring with the identity
. In a distributively-generated near-ring with the identity
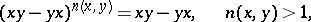 |
multiplication is commutative (cf. [3], [4]).
Every near-ring from 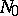 without nilpotent elements is a subdirect product of near-rings without divisors of zero [4]. A near-algebra
without nilpotent elements is a subdirect product of near-rings without divisors of zero [4]. A near-algebra 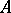 can be decomposed into a direct sum of simple near-rings if and only if: a) it satisfies the minimum condition for principal ideals; b)
can be decomposed into a direct sum of simple near-rings if and only if: a) it satisfies the minimum condition for principal ideals; b) 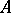 does not contain ideals with zero multiplication; and c) any annihilator of any minimal ideal is maximal [1].
does not contain ideals with zero multiplication; and c) any annihilator of any minimal ideal is maximal [1].
For near-rings one can prove results similar to those on the structure of regular rings [2] and on near-rings of fractions [5]. Near-rings have applications in the study of permutation groups, block-schemes and projective geometry [4].
References
| [1] | H.E. Bell, "A commutativity theorem for near-rings" Canad. Math. Bull. , 20 : 1 (1977) pp. 25–28 |
| [2] | H.E. Heatherly, "Regular near-rings" J. Indian Math. Soc. , 38 (1974) pp. 345–354 |
| [3] | S. Ligh, "The structure of certain classes of rings and near rings" J. London Math. Soc. , 12 : 1 (1975) pp. 27–31 |
| [4] | G. Pilz, "Near-rings" , North-Holland (1983) |
| [5] | A. Oswald, "On near-rings of quotients" Proc. Edinburgh Math. Soc. , 22 : 2 (1979) pp. 77–86 |
| [6] | S.V. Polin, "Generalizations of rings" , Rings , 1 , Novosibirsk (1973) pp. 41–45 (In Russian) |
| [7] | J.D.P. Meldrum, "Near-rings and their links with groups" , Pitman (1985) |
Near-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Near-ring&oldid=15999