Natural exponential family of probability distributions
Given a finite-dimensional real linear space 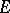 , denote by
, denote by 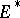 the space of linear forms
the space of linear forms 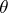 from
from  to
to 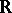 . Let
. Let 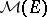 be the set of positive Radon measures
be the set of positive Radon measures 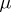 on
on 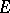 with the following two properties (cf. also Radon measure):
with the following two properties (cf. also Radon measure):
i) 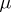 is not concentrated on some affine hyperplane of
is not concentrated on some affine hyperplane of 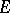 ;
;
ii) considering the interior 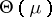 of the convex set of those
of the convex set of those 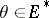 such that
such that
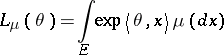 |
is finite, then 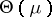 is not empty. For notation, see also Exponential family of probability distributions.
is not empty. For notation, see also Exponential family of probability distributions.
For 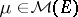 , the cumulant function
, the cumulant function 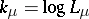 is a real-analytic strictly convex function defined on
is a real-analytic strictly convex function defined on 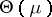 . Thus, its differential
. Thus, its differential
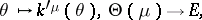 |
is injective. Denote by  its image, and by
its image, and by 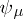 the inverse mapping of
the inverse mapping of 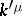 from
from 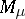 onto
onto 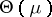 . The natural exponential family of probability distributions (abbreviated, NEF) generated by
. The natural exponential family of probability distributions (abbreviated, NEF) generated by  is the set
is the set 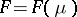 of probabilities
of probabilities
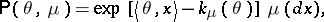 |
when 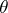 varies in
varies in 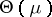 . Note that
. Note that 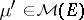 is such that the two sets
is such that the two sets 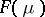 and
and  coincide if and only if there exist an
coincide if and only if there exist an 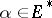 and a
and a 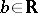 such that
such that 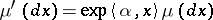 . The mean of
. The mean of 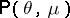 is given by
is given by
 |
and for this reason 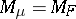 is called the domain of the means of
is called the domain of the means of 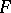 . It is easily seen that it depends on
. It is easily seen that it depends on 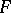 and not on a particular
and not on a particular 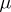 generating
generating 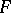 . Also,
. Also,
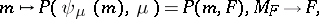 |
is the parametrization of the natural exponential family by the mean. The domain of the means is contained in the interior 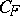 of the convex hull of the support of
of the convex hull of the support of 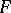 . When
. When  , the natural exponential family is said to be steep. A sufficient condition for steepness is that
, the natural exponential family is said to be steep. A sufficient condition for steepness is that 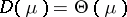 . The natural exponential family generated by a stable distribution in
. The natural exponential family generated by a stable distribution in 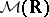 with parameter
with parameter 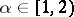 provides an example of a non-steep natural exponential family. A more elementary example is given by
provides an example of a non-steep natural exponential family. A more elementary example is given by 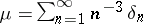 .
.
For one observation 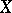 , the maximum-likelihood estimator (cf. also Maximum-likelihood method) of
, the maximum-likelihood estimator (cf. also Maximum-likelihood method) of 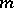 is simply
is simply  : it has to be in
: it has to be in 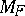 to be defined, and in this case the maximum-likelihood estimator of the canonical parameter
to be defined, and in this case the maximum-likelihood estimator of the canonical parameter  is
is 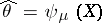 . In the case of
. In the case of  observations,
observations, 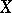 has to be replaced by
has to be replaced by 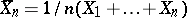 . Note that since
. Note that since 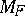 is an open set, and from the strong law of large numbers, almost surely there exists an
is an open set, and from the strong law of large numbers, almost surely there exists an 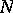 such that
such that 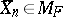 for
for 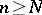 and finally
and finally  will be well-defined after enough observations.
will be well-defined after enough observations.
Exponential families have also a striking property in information theory. That is, they minimize the entropy in the following sense: Let 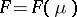 be a natural exponential family on
be a natural exponential family on 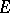 and fix
and fix 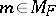 . Let
. Let 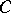 be the convex set of probabilities
be the convex set of probabilities 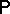 on
on 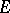 which are absolutely continuous with respect to
which are absolutely continuous with respect to 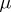 and such that
and such that 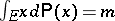 . Then the minimum of
. Then the minimum of 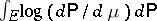 on
on 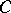 is reached on the unique point
is reached on the unique point 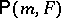 . Extension to general exponential families is trivial. See, e.g., [a5], 3(A).
. Extension to general exponential families is trivial. See, e.g., [a5], 3(A).
Denote by 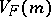 the covariance operator of
the covariance operator of  . The space of symmetric linear operators from
. The space of symmetric linear operators from 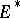 to
to 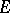 is denoted by
is denoted by 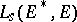 , and the mapping from
, and the mapping from 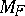 to
to 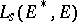 defined by
defined by 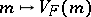 is called the variance function of the natural exponential family
is called the variance function of the natural exponential family 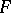 .
.
Because it satisfies the relation 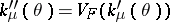 , the variance function
, the variance function 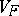 determines the natural exponential family
determines the natural exponential family 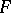 . For each
. For each 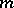 ,
, 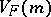 is a positive-definite operator. The variance function also satisfies the following condition: For all
is a positive-definite operator. The variance function also satisfies the following condition: For all 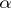 and
and 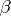 in
in 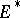 one has
one has
 |
For dimension one, the variance function provides an explicit formula for the large deviations theorem: If 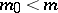 are in
are in 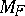 , and if
, and if  are independent real random variables with the same distribution
are independent real random variables with the same distribution 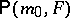 , then
, then
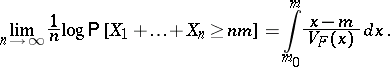 |
The second member can be easily computed for natural exponential families on 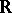 whose variance functions are simple. It happens that a kind of vague principle like "the simpler VF is, more useful is F" holds. C. Morris [a9] has observed that
whose variance functions are simple. It happens that a kind of vague principle like "the simpler VF is, more useful is F" holds. C. Morris [a9] has observed that 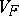 is the restriction to
is the restriction to 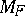 of a polynomial of degree
of a polynomial of degree  if and only if
if and only if 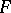 is either normal, Poisson, binomial, negative binomial, gamma, or hyperbolic (i.e., with a Fourier transform
is either normal, Poisson, binomial, negative binomial, gamma, or hyperbolic (i.e., with a Fourier transform 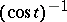 ), at least up to an affinity and a convolution power. Similarly, in [a8], the classification in
), at least up to an affinity and a convolution power. Similarly, in [a8], the classification in  types of the variance functions which are third-degree polynomials is performed: the corresponding distributions are also classical, but occur in the literature as distributions of stopping times of Lévy processes or random walks in
types of the variance functions which are third-degree polynomials is performed: the corresponding distributions are also classical, but occur in the literature as distributions of stopping times of Lévy processes or random walks in 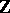 (cf. also Random walk; Stopping time). Other classes, like
(cf. also Random walk; Stopping time). Other classes, like  or
or 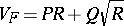 , where
, where  ,
, 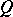 ,
, 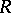 are polynomials of low degree, have also been classified (see [a1] and [a7]).
are polynomials of low degree, have also been classified (see [a1] and [a7]).
In higher dimensions the same principle holds. For instance, M. Casalis [a3] has shown that 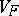 is homogeneous of degree
is homogeneous of degree  if and only if
if and only if  is a family of Wishart distributions on a Euclidean Jordan algebra. She [a4] has also found the
is a family of Wishart distributions on a Euclidean Jordan algebra. She [a4] has also found the  types of natural exponential families on
types of natural exponential families on 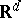 whose variance function is
whose variance function is  , where
, where 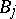 and
and  are real
are real 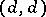 -matrices and
-matrices and 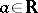 , thus providing a generalization of the above-mentioned result by Morris. Another extension is obtained in [a2], where all non-trivial natural exponential families in
, thus providing a generalization of the above-mentioned result by Morris. Another extension is obtained in [a2], where all non-trivial natural exponential families in  whose marginal distributions are still natural exponential families are found; surprisingly, these marginal distributions are necessarily of Morris type.
whose marginal distributions are still natural exponential families are found; surprisingly, these marginal distributions are necessarily of Morris type.
Finally, the cubic class is generalized in a deep way to 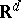 in [a6].
in [a6].
References
| [a1] | S. Bar-Lev, P. Enis, "Reproducibility and natural exponential families with power variance functions" Ann. Statist. , 14 (1987) pp. 1507–1522 |
| [a2] | S. Bar-Lev, D. Bshouty, P. Enis, G. Letac, I-Li Lu, D. Richards, "The diagonal multivariate natural exponential families and their classification" J. Theor. Probab. , 7 (1994) pp. 883–929 |
| [a3] | M. Casalis, "Les familles exponentielles à variance quadratique homogæne sont des lois de Wishart sur un c spone symétrisque" C.R. Acad. Sci. Paris Ser. I , 312 (1991) pp. 537–540 |
| [a4] | M. Casalis, "The 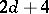 simple quadratic natural exponential families on simple quadratic natural exponential families on 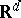 " Ann. Statist. , 24 (1996) pp. 1828–1854 " Ann. Statist. , 24 (1996) pp. 1828–1854 |
| [a5] | I. Csiszár, "I-Divergence, geometry of probability distributions, and minimization problems" Ann. of Probab. , 3 (1975) pp. 146–158 |
| [a6] | A. Hassaïri, "La classification des familles exponentielles naturelles sur 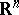 par l'action du groupe linéaire de par l'action du groupe linéaire de 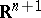 " C.R. Acad. Sci. Paris Ser. I , 315 (1992) pp. 207–210 " C.R. Acad. Sci. Paris Ser. I , 315 (1992) pp. 207–210 |
| [a7] | C. Kokonendji, "Sur les familles exponentielles naturelles de grand-Babel" Ann. Fac. Sci. Toulouse , 4 (1995) pp. 763–800 |
| [a8] | G. Letac, M. Mora, "Natural exponential families with cubic variance functions" Ann. Statist. , 18 (1990) pp. 1–37 |
| [a9] | C.N. Morris, "Natural exponential families with quadratic variance functions" Ann. Statist. , 10 (1982) pp. 65–80 |
Natural exponential family of probability distributions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Natural_exponential_family_of_probability_distributions&oldid=16396