Nash theorems (in differential geometry)
Two groups of theorems on isometrically imbedded and immersed Riemannian manifolds in a Euclidean space (see also Immersion of a manifold; Isometric immersion). The original versions are due to J. Nash [1].
1) Nash' theorem on 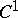 -imbeddings and
-imbeddings and 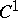 -immersions. An immersion (imbedding)
-immersions. An immersion (imbedding) 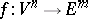 of class
of class 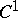 of an
of an  -dimensional Riemannian space
-dimensional Riemannian space 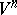 with metric
with metric 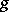 of class
of class 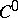 into an
into an 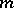 -dimensional Euclidean space
-dimensional Euclidean space 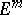 is called short if the metric
is called short if the metric 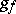 induced by it on
induced by it on 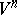 is such that the quadratic form
is such that the quadratic form 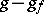 is positive definite. If
is positive definite. If 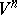 has a short immersion (imbedding) in
has a short immersion (imbedding) in 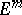 ,
, 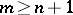 , then
, then 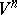 also has an isometric immersion (imbedding) of class
also has an isometric immersion (imbedding) of class 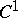 in
in 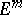 . Under the restriction
. Under the restriction 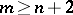 this theorem was proved in [1], and in the form stated above in [2]. This theorem implies, in particular, that if a compact Riemannian manifold
this theorem was proved in [1], and in the form stated above in [2]. This theorem implies, in particular, that if a compact Riemannian manifold 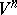 has a
has a 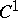 -imbedding (immersion) in
-imbedding (immersion) in 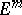 ,
, 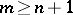 , then
, then 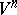 also has an isometric
also has an isometric 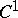 -imbedding (immersion) in
-imbedding (immersion) in 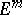 . Another consequence of Nash' theorem is that every point of
. Another consequence of Nash' theorem is that every point of 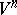 has a sufficiently small neighbourhood that admits an isometric imbedding of class
has a sufficiently small neighbourhood that admits an isometric imbedding of class 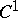 in
in 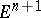 .
.
2) Nash' theorem on regular imbeddings. Every compact Riemannian manifold 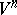 of class
of class 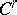 ,
, 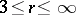 , has an isometric
, has an isometric 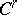 -imbedding in
-imbedding in 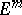 , where
, where 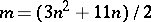 . If
. If 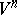 is not compact, then it has an isometric
is not compact, then it has an isometric 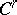 -imbedding in
-imbedding in 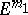 , where
, where 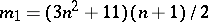 .
.
Nash' theorem on regular imbeddings results from an application of Nash' implicit-function theorem on the inversion of a broad class of differential operators. The meaning of this theorem is that when a certain linear algebraic system of equations connected naturally with a differential operator 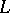 is solvable and when a reasonable topology is introduced in the image and inverse image, then the operator in question is an open mapping, that is,
is solvable and when a reasonable topology is introduced in the image and inverse image, then the operator in question is an open mapping, that is, 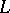 is locally invertible near any point of its range. For the equations of an imbedding of a Riemannian manifold in a Euclidean space this reduces to the fact that the first and second derivatives of the mapping
is locally invertible near any point of its range. For the equations of an imbedding of a Riemannian manifold in a Euclidean space this reduces to the fact that the first and second derivatives of the mapping 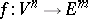 with respect to the intrinsic coordinates of
with respect to the intrinsic coordinates of 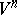 must be linearly independent. Such imbeddings were first considered in [4]; they are called free. Nash' implicit-function theorem implies that a compact Riemannian manifold
must be linearly independent. Such imbeddings were first considered in [4]; they are called free. Nash' implicit-function theorem implies that a compact Riemannian manifold 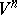 sufficiently close to another one
sufficiently close to another one 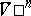 having a free imbedding in
having a free imbedding in 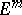 also has a free imbedding in
also has a free imbedding in 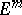 . This fact and the original method of extension with respect to a parameter lead to Nash' theorem on regular imbeddings (see [3]). By extending Nash' method to non-compact manifolds and analytic imbeddings, and also by a principal refinement of the process of extension with respect to a parameter, it has been proved that every infinitely-differentiable (analytic) Riemannian manifold
. This fact and the original method of extension with respect to a parameter lead to Nash' theorem on regular imbeddings (see [3]). By extending Nash' method to non-compact manifolds and analytic imbeddings, and also by a principal refinement of the process of extension with respect to a parameter, it has been proved that every infinitely-differentiable (analytic) Riemannian manifold 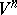 has an isometric differentiable (analytic) imbedding in
has an isometric differentiable (analytic) imbedding in 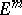 , where
, where 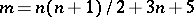 (see [5]–[7]).
(see [5]–[7]).
References
| [1] | J. Nash, "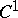 -isometric imbeddings" Ann. of Math. , 60 (1954) pp. 383–396 -isometric imbeddings" Ann. of Math. , 60 (1954) pp. 383–396 |
| [2] | N. Kuiper, "On 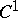 -isometric imbeddings" Proc. K. Ned. Akad. Wetensch. , A58 : 4 (1955) pp. 545–556 -isometric imbeddings" Proc. K. Ned. Akad. Wetensch. , A58 : 4 (1955) pp. 545–556 |
| [3] | J. Nash, "The imbedding problem for Riemannian manifolds" Ann. of Math. , 63 (1956) pp. 20–63 |
| [4] | C. Burstin, "Ein Beitrag zum Problem der Einbettung der Riemannschen Räume in euklidischen Räumen" Mat. Sb. , 38 : 3–4 (1931) pp. 74–85 |
| [5] | J. Nash, "Analyticity of the solutions of implicit function problems with analytic data" Ann. of Math. , 84 (1966) pp. 345–355 |
| [6] | M.L. Gromov, V.A. Rokhlin, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–57 Uspekhi Mat. Nauk , 25 (1970) pp. 53–62 |
| [7] | M.L. Gromov, "Isometric imbeddings and immersions" Soviet Math. Dokl. , 11 : 3 (1970) pp. 1206–1209 Dokl. Akad. Nauk SSSR , 192 (1970) pp. 794–797 |
Comments
The Nash theorem in differential topology says that a compact connected 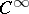 -manifold without boundary is diffeomorphic to a component of a real algebraic variety.
-manifold without boundary is diffeomorphic to a component of a real algebraic variety.
Let 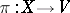 be a smooth (i.e.
be a smooth (i.e. 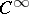 -) fibration. Denote by
-) fibration. Denote by 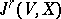 the space of
the space of  -jets (of germs) of smooth sections
-jets (of germs) of smooth sections 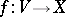 (cf. Germ; Jet). The
(cf. Germ; Jet). The  -th order jet of a section
-th order jet of a section 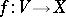 is denoted by
is denoted by 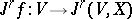 . A section
. A section 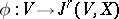 is called holonomic if there is a
is called holonomic if there is a 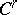 -section
-section 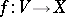 such that
such that 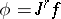 ;
; 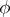 determines
determines 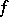 uniquely (if it exists). The fine topology on the space
uniquely (if it exists). The fine topology on the space 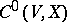 of
of 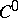 -sections
-sections 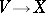 is obtained by taking as a basis the subsets
is obtained by taking as a basis the subsets 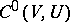 where
where 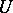 runs over the open subsets of
runs over the open subsets of 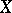 . The fine
. The fine 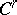 -topology on
-topology on 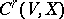 is induced by the imbedding
is induced by the imbedding 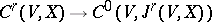 ,
, 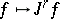 , from the fine
, from the fine 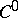 -topology to
-topology to 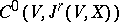 .
.
The Nash approximation theorem says that an arbitrary Riemannian 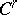 -metric on
-metric on 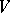 has a fine
has a fine 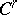 -approximation by some
-approximation by some 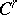 -metric
-metric 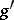 on
on 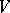 that admits
that admits 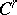 -immersions
-immersions 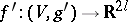 for some
for some 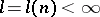 , where
, where 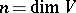 .
.
The Nash–Kuiper theorem [1], [2] says that an arbitrary differentiable immersion 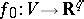 for
for 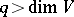 admits a
admits a 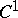 -continuous homotopy of immersions
-continuous homotopy of immersions 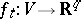 ,
, 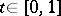 , to an isometric immersion
, to an isometric immersion 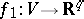 .
.
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) |
| [a2] | M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) |
Nash theorems (in differential geometry). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorems_(in_differential_geometry)&oldid=12150