Nash theorem (in game theory)
From Encyclopedia of Mathematics
A theorem on the existence of equilibrium points in a mixed extension of a finite non-cooperative game
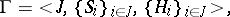 |
where 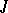 and
and 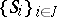 are the finite sets of players and their strategies, respectively, and
are the finite sets of players and their strategies, respectively, and 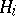 :
: 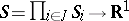 is the pay-off function of player
is the pay-off function of player 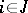 (see also Games, theory of). It was established by J. Nash in [1]. Let
(see also Games, theory of). It was established by J. Nash in [1]. Let 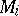 ,
, 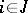 , be the set of all probability measures on
, be the set of all probability measures on 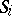 . Nash' theorem asserts that there is a measure
. Nash' theorem asserts that there is a measure 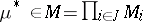 for which
for which
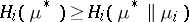 |
for all 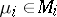 ,
, 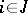 , where
, where 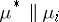 denotes the measure from
denotes the measure from 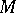 that results from replacing the
that results from replacing the 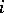 -th component of the vector
-th component of the vector 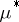 by
by 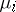 , and
, and 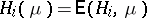 . The known proofs of Nash' theorem rely on a fixed-point theorem.
. The known proofs of Nash' theorem rely on a fixed-point theorem.
References
| [1] | J. Nash, "Non-cooperative games" Ann. of Math. , 54 (1951) pp. 286–295 |
| [2] | N.N. Vorob'ev, "Foundations of game theory. Non-cooperative games" , Moscow (1984) (In Russian) |
| [3] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
How to Cite This Entry:
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=18406
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=18406
This article was adapted from an original article by E.B. Yanovskaya (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article