N-group
A generalization of the concept of a group to the case of an  -ary operation. An
-ary operation. An  -group is a universal algebra with one
-group is a universal algebra with one  -ary associative operation that is uniquely invertible at each place (cf. Algebraic operation). The theory of
-ary associative operation that is uniquely invertible at each place (cf. Algebraic operation). The theory of  -groups for
-groups for 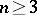 substantially differs from the theory of groups (i.e.
substantially differs from the theory of groups (i.e.  -groups). Thus, if
-groups). Thus, if 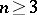 , an
, an  -group has no analogue of the unit element.
-group has no analogue of the unit element.
Let 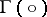 be a group with multiplication operation
be a group with multiplication operation  ; let
; let 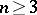 be an arbitrary integer. Then an
be an arbitrary integer. Then an  -ary operation
-ary operation 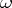 on the set
on the set 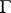 can be defined as follows:
can be defined as follows:
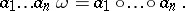 |
The resulting  -group is called the
-group is called the  -group determined by the group
-group determined by the group 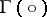 . Necessary and sufficient conditions for an
. Necessary and sufficient conditions for an  -group to be of this form are known [1]. Any
-group to be of this form are known [1]. Any  -group is imbeddable in such an
-group is imbeddable in such an  -group (Post's theorem).
-group (Post's theorem).
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Comments
The usual notion of a 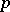 -group (i.e., a group of order a power of
-group (i.e., a group of order a power of 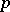 ) is not to be mixed up with that of an
) is not to be mixed up with that of an  -group in the above sense.
-group in the above sense.
References
| [a1] | D. Balci, "Zur Theorie der topologischen  -Gruppen" , Minerva , Munich (1981) -Gruppen" , Minerva , Munich (1981) |
| [a2] | S.A. Rusakov, "The subgroup structure of Dedekind  -ary groups" , Finite groups (Proc. Gomel. Sem.) , Minsk (1978) pp. 81–104 (In Russian) -ary groups" , Finite groups (Proc. Gomel. Sem.) , Minsk (1978) pp. 81–104 (In Russian) |
| [a3] | S.A. Rusakov, "On the theory of nilpotent  -ary groups" , Finite groups (Proc. Gomel. Sem.) , Minsk (1978) pp. 104–130 (In Russian) -ary groups" , Finite groups (Proc. Gomel. Sem.) , Minsk (1978) pp. 104–130 (In Russian) |
N-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=N-group&oldid=17675