Néron model
of an Abelian variety
A group scheme associated to an Abelian variety and having a certain minimality property. If 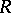 is a local Henselian discrete valuation ring with residue field
is a local Henselian discrete valuation ring with residue field 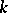 and field of fractions
and field of fractions 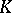 and if
and if  is an Abelian variety of dimension
is an Abelian variety of dimension 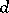 over
over 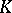 , then a Néron model of
, then a Néron model of  is defined as a smooth commutative group scheme
is defined as a smooth commutative group scheme 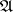 over
over 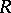 whose generic fibre
whose generic fibre 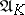 is isomorphic to
is isomorphic to 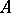 , while the canonical homomorphism
, while the canonical homomorphism 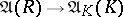 is an isomorphism. This concept was introduced by A. Néron [1] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an
is an isomorphism. This concept was introduced by A. Néron [1] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an 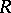 -isomorphism. A Néron model has the following minimality property: For any smooth
-isomorphism. A Néron model has the following minimality property: For any smooth 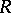 -scheme
-scheme 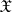 and any morphism
and any morphism  of the generic fibres there exists a unique morphism
of the generic fibres there exists a unique morphism 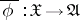 of
of  -schemes induced by
-schemes induced by 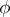 .
.
If 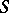 is a one-dimensional regular Noetherian scheme,
is a one-dimensional regular Noetherian scheme, 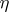 is a generic point of it,
is a generic point of it, 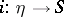 is its canonical imbedding, and
is its canonical imbedding, and  is an Abelian variety over
is an Abelian variety over 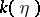 , then a Néron model of
, then a Néron model of 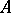 is defined as a smooth quasi-projective group scheme
is defined as a smooth quasi-projective group scheme 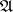 over
over 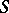 that represents the sheaf
that represents the sheaf 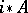 relative to the flat Grothendieck topology on
relative to the flat Grothendieck topology on 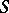 (see [4]).
(see [4]).
For a generalization of the concept of a Néron model to arbitrary schemes see [3].
References
| [1] | A. Néron, "Modèles minimaux des variétés abéliennes sur les corps locaux et globaux" Publ. Math. IHES , 21 (1964) |
| [2] | B. Mazur, "Rational points of Abelian varieties with values in towers of number fields" Invent. Math. , 18 (1974) pp. 183–266 |
| [3] | M. Raynaud, "Modèles de Néron" C.R. Acad. Sci. Paris Sér. A , 262 (1966) pp. 345–347 |
| [4] | M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 12–30 |
| [5] | A. Grothendieck (ed.) et al. (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7 , Lect. notes in math. , 288 , Springer (1972) |
Comments
References
| [a1] | M. Artin, "Néron models" G. Cornell (ed.) J. Silverman (ed.) , Arithmetic geometry , Springer (1986) pp. 213–230 |
Néron model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=N%C3%A9ron_model&oldid=12071