Néron-Severi group
The divisor class group under algebraic equivalence on a non-singular projective variety.
Let  be a non-singular projective variety of dimension
be a non-singular projective variety of dimension  defined over an algebraically closed field
defined over an algebraically closed field  , let
, let  be the group of divisors of
be the group of divisors of  and let
and let  be the subgroup of divisors that are algebraically equivalent to zero. The quotient group
be the subgroup of divisors that are algebraically equivalent to zero. The quotient group  is called the Néron–Severi group of
is called the Néron–Severi group of  and is denoted by
and is denoted by  . The Néron–Severi theorem asserts that the Abelian group
. The Néron–Severi theorem asserts that the Abelian group 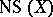 is finitely generated.
is finitely generated.
In the case 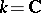 , F. Severi presented, in a series of papers on the theory of the base (see, for example, [1]), a proof of this theorem using topological and transcendental tools. The first abstract proof (valid for a field of arbitrary characteristic) is due to A. Néron (see [2], [3], and also [4]).
, F. Severi presented, in a series of papers on the theory of the base (see, for example, [1]), a proof of this theorem using topological and transcendental tools. The first abstract proof (valid for a field of arbitrary characteristic) is due to A. Néron (see [2], [3], and also [4]).
The rank of 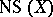 is the algebraic Betti number of the group of divisors on
is the algebraic Betti number of the group of divisors on  , that is, the algebraic rank of
, that is, the algebraic rank of  . This is also called the Picard number of the variety
. This is also called the Picard number of the variety  . The elements of the finite torsion subgroup
. The elements of the finite torsion subgroup 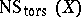 are called Severi divisors, and the order of this subgroup is called the Severi number; the group
are called Severi divisors, and the order of this subgroup is called the Severi number; the group 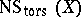 is a birational invariant (see [6]).
is a birational invariant (see [6]).
There are generalizations of the Néron–Severi theorem to other groups of classes of algebraic cycles (see [1] (classical theory) and [7] (modern theory)).
References
| [1] | F. Severi, "La base per le varietà algebriche di dimensione qualunque contenute in una data e la teoria generale delle corrispondénze fra i punti di due superficie algebriche" Mem. Accad. Ital. , 5 (1934) pp. 239–283 |
| [2] | A. Néron, "Problèmes arithmétiques et géometriques attachée à la notion de rang d'une courbe algébrique dans un corps" Bull. Soc. Math. France , 80 (1952) pp. 101–166 |
| [3] | A. Néron, "La théorie de la base pour les diviseurs sur les variétés algébriques" ,  Coll. Géom. Alg. Liège , G. Thone (1952) pp. 119–126 Coll. Géom. Alg. Liège , G. Thone (1952) pp. 119–126 |
| [4] | S. Lang, A. Néron, "Rational points of abelian varieties over function fields" Amer. J. Math. , 81 (1959) pp. 95–118 |
| [5] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [6] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [7] | I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" J. Soviet Math. , 5 : 6 (1976) pp. 803–864 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 12 (1974) pp. 77–170 |
Comments
A study of the Picard number of a certain number of algebraic varieties has been made by T. Shioda.
The phrase "theory of the basetheory of the base" is a somewhat old-fashioned one and refers to the considerations involved in proving that 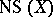 is a finitely-generated Abelian group and indicating an explicit minimal set of generators (a minimal base in the terminology of Severi), cf. e.g. [a4], Sect. V.7 (for the case of surfaces).
is a finitely-generated Abelian group and indicating an explicit minimal set of generators (a minimal base in the terminology of Severi), cf. e.g. [a4], Sect. V.7 (for the case of surfaces).
References
| [a1] | T. Shioda, "On the Picard number of a complex projective variety" Ann. Sci. Ecole Norm. Sup. , 14 (1981) pp. 303–321 |
| [a2] | T. Shioda, "On the Picard number of a Fermat surface" J. Fac. Sci. Univ. Tokyo , 28 (1982) pp. 724–734 |
| [a3] | T. Shioda, "An explicit algorithm for computing the Picard number of certain algebraic surfaces" Amer. J. Math. , 108 (1986) pp. 415–432 |
| [a4] | O. Zariski, "Algebraic surfaces" , Springer (1935) |
Néron-Severi group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=N%C3%A9ron-Severi_group&oldid=17702