Multiply-connected domain
in a path-connected space
A domain 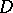 in which there are closed paths not homotopic to zero, or, in other words, whose fundamental group is not trivial. This means that there are closed paths in
in which there are closed paths not homotopic to zero, or, in other words, whose fundamental group is not trivial. This means that there are closed paths in 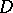 which cannot be continuously deformed to a point while remaining throughout within
which cannot be continuously deformed to a point while remaining throughout within  , or, otherwise, a multiply-connected domain
, or, otherwise, a multiply-connected domain 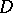 is a domain which is not a simply-connected domain.
is a domain which is not a simply-connected domain.
The order of connectivity of a plane domain 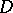 in
in 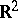 or
or 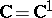 (or in the compactification of these spaces,
(or in the compactification of these spaces, 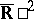 or
or 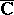 ) is the number of (homologically) independent one-dimensional cycles, that is, the one-dimensional Betti number
) is the number of (homologically) independent one-dimensional cycles, that is, the one-dimensional Betti number 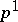 of
of 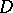 . If the number
. If the number 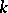 of connected components of the boundary of a plane domain
of connected components of the boundary of a plane domain 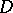 , considered as a domain in the compactified space
, considered as a domain in the compactified space 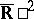 or
or 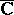 , is finite, then
, is finite, then 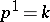 ; otherwise one sets
; otherwise one sets 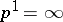 . When
. When 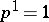 ,
, 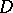 is a simply-connected domain, when
is a simply-connected domain, when 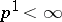 it is a finitely-connected domain (one also uses such terms as doubly-connected domain, triply-connected domain
it is a finitely-connected domain (one also uses such terms as doubly-connected domain, triply-connected domain
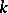 -connected domain), when
-connected domain), when 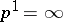 ,
, 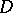 is an infinitely-connected domain. All plane finitely-connected domains with equal order of connectivity,
is an infinitely-connected domain. All plane finitely-connected domains with equal order of connectivity, 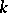 , are homeomorphic to each other. By removing from such a domain
, are homeomorphic to each other. By removing from such a domain 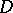 all the points of
all the points of 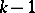 cuts, that is, Jordan arcs joining pairs of connected components of the boundary, it is always possible to obtain a simply-connected domain
cuts, that is, Jordan arcs joining pairs of connected components of the boundary, it is always possible to obtain a simply-connected domain 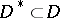 . About the conformal types of plane multiply-connected domains see Riemann surfaces, conformal classes of.
. About the conformal types of plane multiply-connected domains see Riemann surfaces, conformal classes of.
The topological types of domains in 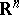 ,
, 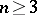 , or
, or 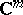 ,
,  , are far more diverse and cannot be characterized by a single number. Here, sometimes, the term "multiply-connected domain" (with various provisos) is used when the fundamental group is trivial but some higher-dimensional homology group is not trivial.
, are far more diverse and cannot be characterized by a single number. Here, sometimes, the term "multiply-connected domain" (with various provisos) is used when the fundamental group is trivial but some higher-dimensional homology group is not trivial.
Comments
For a discussion of non-planar multiply-connected domains see [a1].
There are two rather different concepts which go by the phrase "multi-connected spacemulti-connected" or "multiply-connected" . The concept and terminology as described above come from the theory of functions of a complex variable.
On the other hand, in (algebraic) topology one defines an  -connected space as a space
-connected space as a space 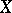 such that any mapping from a sphere
such that any mapping from a sphere 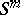 ,
, 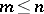 , into
, into  is homotopic to zero. Thus,
is homotopic to zero. Thus,  -connectedness is the same as path connectedness.
-connectedness is the same as path connectedness.
References
| [a1] | G.K. Francis, "A topological picturebook" , Springer (1987) |
| [a2] | W.S. Massey, "Algebraic topology: an introduction" , Springer (1967) |
| [a3] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 23; 415–455 |
Multiply-connected domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiply-connected_domain&oldid=13135