Multipliers-of-C*-algebras
A $C ^ { * }$-algebra $A$ of operators on some Hilbert space $\mathcal{H}$ may be viewed as a non-commutative generalization of a function algebra $C _ { 0 } ( \Omega )$ acting as multiplication operators on some $L^{2}$-space associated with a measure on the locally compact space $\Omega$. The space $\Omega$ being compact corresponds naturally to the case where the algebra $A$ is unital. In the non-unital case any embedding of $A$ as an essential ideal in some larger unital $C ^ { * }$-algebra $B$ (i.e., the annihilator of $A$ in $B$ is zero) can be viewed as an analogue of a compactification of the locally compact Hausdorff space $\Omega$. Thus, the one-point compactification $\Omega \cup \{ \infty \}$ of $\Omega$ corresponds to the unitization $\tilde { A } = A \oplus \mathbf{C}$ of the algebra $A$. The analogue of the maximal compactification — the Stone–Čech compactification — is the algebra $M ( A )$ of multipliers of $A$, defined by R.C. Busby in 1967 [a4] and studied in more detail in [a2]. It is defined simply as the idealizer of $A$ in $B ( \mathcal{H} )$ (assuming that $A \mathcal{H} = \mathcal{H}$ or, equivalently, that no non-zero vector in $\mathcal{H}$ is annihilated by $A$).
Linear operators $\lambda$ and $\rho$ on $A$ are called left and right centralizers if $\lambda ( x y ) = \lambda ( x ) y$ and $\rho ( x y ) = x \rho ( y )$ for all $x$, $y$ in $A$. They are automatically bounded. A double centralizer is a pair $( \lambda , \rho )$ of left, right centralizers such that $x \lambda ( y ) = \rho ( x ) y$ (whence $\| \lambda \| = \| \rho \|$), and the closed linear spaces of double centralizers becomes a $C ^ { * }$-algebra when product and involution are defined by $( \lambda _ { 1 } , \rho _ { 1 } ) ( \lambda _ { 2 } , \rho _ { 2 } ) = ( \lambda _ { 1 } \lambda _ { 2 } , \rho _ { 2 } \rho _ { 1 } )$ and $( \lambda , \rho ) ^ { * } = ( \rho ^ { * } , \lambda ^ { * } )$ (where $\lambda ^ { * } ( x ) = ( \lambda ( x ^ { * } ) ) ^ { * }$). As shown by B.E. Johnson, [a8], there is an isomorphism between the abstractly defined $C ^ { * }$-algebra of double centralizers of $A$ and the concrete $C ^ { * }$-algebra $M ( A )$. This, in particular, shows that $M ( A )$ is independent of the given representation of $A$ on $\mathcal{H}$.
The strict topology on $M ( A )$ is defined by the semi-norms $x \rightarrow \| a x \| + \| a x \|$ on $B ( \mathcal{H} )$ with $a$ in $A$, [a4]. It is used as an analogue of uniform convergence on compact subsets of $\Omega$ in function algebras. Thus, it can be shown that $M ( A )$ is the strict completion of $A$ in $B ( \mathcal{H} )$ and that the strict dual of $M ( A )$ equals the norm dual of $A$, [a16].
If $\mathcal{H}$ is the universal Hilbert space for $A$ (the orthogonal sum of all Hilbert spaces obtained from states of $A$ via the Gel'fand–Naimark–Segal construction), then $M ( A )$ has a more constructive characterization: Let 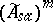 denote the space of self-adjoint operators in $B ( \mathcal{H} )$ that can be obtained as limits (in the strong topology) of some increasing net of self-adjoint elements from the unitized algebra $\tilde{A}$ (cf. also Net (directed set); Self-adjoint operator). Similarly, let
denote the space of self-adjoint operators in $B ( \mathcal{H} )$ that can be obtained as limits (in the strong topology) of some increasing net of self-adjoint elements from the unitized algebra $\tilde{A}$ (cf. also Net (directed set); Self-adjoint operator). Similarly, let 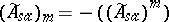 be the space of limits of decreasing nets. Then
be the space of limits of decreasing nets. Then
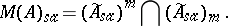 |
Thus, for every self-adjoint multiplier $x$ there are nets $( a _\lambda )$ and $( b _ { \mu } )$ in $\widetilde { A } _ { s a }$, one increasing, the other decreasing, such that $a_{\lambda} \nearrow x \swarrow b _ { \mu }$. If $A$ is $\sigma$-unital, i.e. contains a countable approximate unit, in particular if $A$ is separable (cf. also Separable algebra), these nets can be taken as sequences, [a2], [a12], p. 12. In the commutative case, where $A = C _ { 0 } ( \Omega )$, whence $M ( A ) = C _ { b } ( \Omega )$, this expresses the well-known fact that a bounded, real function on $\Omega$ is continuous precisely when it is both lower and upper semi-continuous.
For any $C ^ { * }$-algebra $X$ containing $A$ as an ideal there is a natural morphism (i.e. a $\square ^ { * }$-homomorphism) $\sigma : X \rightarrow M ( A )$, defined by $\sigma ( x ) a = x a$, that extends the identity mapping of $A \subset X$ onto $A \subset M ( A )$. If $A$ is essential in $X$, one therefore obtains an embedding $X \subset M ( A )$. Any morphism $\alpha : A \rightarrow B$ between $C ^ { * }$-algebras $A$ and $B$ extends uniquely to a strictly continuous morphism $\overline { \alpha } : M ( A ) \rightarrow M ( B )$, provided that $\alpha$ is proper (i.e. maps an approximate unit for $A$ to one for $B$). Such morphisms are the analogues of proper continuous mappings between locally compact spaces. If $A$ is $\sigma$-unital and $\alpha$ is a quotient morphism, i.e. surjective, then $\overline { \alpha }$ is also surjective. This result may be viewed as a non-commutative generalization of the Tietze extension theorem, [a2], [a13] (cf. also Extension theorems).
The corona of a $C ^ { * }$-algebra $A$ is defined as the quotient $C ^ { * }$-algebra $Q ( A ) = M ( A ) / A$, [a13]. The commutative analogue is the compact Hausdorff space $\beta \ \Omega \ \backslash \ \Omega$ (the corona of the locally compact space $\Omega$, [a6]), but the pre-eminent example of such algebras is the Calkin algebra $B (\mathcal{H} ) / K ( \mathcal{H} )$, obtained by taking $A$ as the algebra $K ( \mathcal{H} )$ of compact operators on $\mathcal{H}$ (whence $M ( A ) = B ( \mathcal{H} )$). Corona $C ^ { * }$-algebras are usually non-separable and cannot even be represented on separable Hilbert spaces, [a14]. Nevertheless, they have important roles in the formulation of G. Kasparov's KK-theory and the later variation known as E-theory. The foremost application, however, is to the theory of extensions: An extension of $C ^ { * }$-algebras $A$ and $B$ is any $C ^ { * }$-algebra $X$ that fits into a short exact sequence (cf. also Exact sequence)
\begin{equation*} 0 \rightarrow A \rightarrow X \stackrel { \pi } { \rightarrow } B \rightarrow 0. \end{equation*}
Thus, $X$ contains $A$ as an ideal, and $\pi$ is simply the quotient morphism. In particular, $M ( A )$ may be regarded as an extension of $A$ by $Q ( A )$, and in fact a maximal such. Namely, any other extension will give rise to a commutative diagram
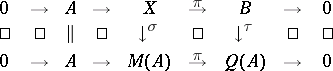 |
Here $\sigma : X \rightarrow M ( A )$ is the morphism defined above and the induced morphism $\tau : B \rightarrow Q ( A )$ is known as the Busby invariant for $X$. This invariant determines $X$ up to an obvious equivalence, because the right square in the diagram above describes $X$ as the pull-back of $B$ and $M ( A )$ over $Q ( A )$, i.e.
\begin{equation*} X = M ( A ) \bigoplus _ { Q ( A ) } B = \end{equation*}
\begin{equation*} = \{ ( m , b ) \in M ( A ) \bigoplus B : \pi ( m ) = \tau ( b ) \}. \end{equation*}
One therefore has the identification $\operatorname { Ext } ( A , B ) = \operatorname { Hom } ( B , Q ( A ) )$, [a4], [a5], [a15].
For any quotient morphism $\pi : X \rightarrow B$ between $C ^ { * }$-algebras one may ask whether an element $b$ in $B$ with specific properties is the image of some $x$ in $X$ with the same properties. This is known as a lifting problem, and is the non-commutative analogue of extension problems for functions. Many lifting problems have positive (and easy) solutions: If $b = b ^ { * }$ or $b \geq 0$ or $\| b \| \leq 1$, one can find counter-images in $X$ with the same properties. However, the properties $b ^ { 2 } = b$ (being idempotent) and $b ^ { * } b = b b ^ { * }$ (being normal) are not liftable in general. It follows that the more general commutator relation $b _ { 1 } b _ { 2 } = b _ { 2 } b _ { 1 }$ is not liftable either. But the orthogonality relation $b _ { 1 } b _ { 2 } = 0$ is liftable (even in the $n$-fold version $b _ { 1 } \ldots b _ { n } = 0$). Using this one may show that the nilpotency relation $b ^ { n } = 0$ is liftable, [a1], [a11], [a9].
As advocated by T.A. Loring, lifting problems may with advantage be replaced by $C ^ { * }$-algebra problems concerning projectivity. A $C ^ { * }$-algebra $P$ is projective if any morphism $\alpha : P \rightarrow B$ into a quotient $C ^ { * }$-algebra $B = \pi ( X )$ can be factored as $\alpha = \pi \circ \overline { \alpha }$ for some morphism $\overline { \alpha } : P \rightarrow X$, [a3]. This means that one is lifting a whole $C ^ { * }$-subalgebra and not just some elements. Projective $C ^ { * }$-algebras are the non-commutative analogues of topological spaces that are absolute retracts, but since the category of $C ^ { * }$-algebras is vastly larger than the category of locally compact Hausdorff spaces, projectivity is a rare phenomenon. However, the cone over the $n \times n$-matrices, i.e. the algebra
\begin{equation*} \mathbf{C M} _ { n } = C _ { 0 } ( ]0,1 ] ) \otimes \mathbf{M} _ { n } \end{equation*}
is always projective. This means that although matrix units cannot, in general, be lifted from quotients, there are lifts in the "smeared" form given by 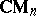 , [a10], [a9].
, [a10], [a9].
Corona $C ^ { * }$-algebras form an indispensable tool for more complicated lifting problems, because by Busby's theory, mentioned above, it suffices to solve the lifting for quotient morphisms of the form $\pi : M ( A ) \rightarrow Q ( A )$. Thus, one may utilize the special properties that corona algebras have. A brief outline of these follows.
Corona algebras.
In topology, a compact Hausdorff space is called sub-Stonean if any two disjoint, open, $\sigma$-compact sets have disjoint closures. Exotic as this may sound, it is a property that any corona set $\beta \ \Omega \ \backslash \ \Omega$ will have, if $\Omega$ is locally compact and $\sigma$-compact. In such a space, every open, $\sigma$-compact subset is also regularly embedded, i.e. it equals the interior of its closure in $\beta \ \Omega \ \backslash \ \Omega$, [a6]. The non-commutative generalization of this is the fact that if $A$ is a $\sigma$-unital $C ^ { * }$-algebra, then every $\sigma$-unital hereditary $C ^ { * }$-subalgebra $B$ of its corona algebra $Q ( A )$ equals its double annihilator, i.e. $B = ( B ^ { \perp } ) ^ { \perp }$, [a13]. The analogue of the sub–Stonean property, sometimes called the $S A W ^ { * }$-condition, is even more striking: For any two orthogonal elements $x$ and $y$ in $Q ( A )$ (say $x y = 0$) there is an element $e$ in $Q ( A )$ with $0 \leq e \leq 1$, such that $x e = x$ and $e y = 0$. Even better, if $C$ and $N$ are separable subsets of $Q ( A )$ such that $x$ commutes with $C$ and annihilates $N$, then the element $e$ can be chosen with the same properties, [a11], [a14]. Note that if $e$ could be taken as a projection, e.g. the range projection of $e$, this would be a familiar property in von Neumann algebra theory. The fact that corona algebras will never be von Neumann algebras (if $A$ is non-unital and $\sigma$-unital) indicates that the property (first established by G. Kasparov as a "technical lemma" ) is useful. Actually, a potentially stronger version is true: If $x _ { n }$ and $y _ { n }$ are monotone sequences of self-adjoint elements in $Q ( A )$, one increasing, the other decreasing, such that $x _ { n } \leq y _ { n }$ for all $n$, and if $C$ and $N$ are separable subsets of $Q ( A )$, such that all $x _ { n }$ commute with $C$ and annihilate $N$, then there is an element $z$ in $Q ( A )$ such that $x _ { n } \leq z \leq y _ { n }$ for all $n$, and $z$ commutes with $C$ and annihilates $N$, [a11]. This has as a consequence that if $B$ is any $\sigma$-unital $C ^ { * }$-subalgebra of $Q ( A )$, commuting with $C$ and annihilating $N$, as above, then for any multiplier $x$ in $M ( B )$ there is an element $z$ in the idealizer $I ( B )$ of $B$ in $Q ( A )$, still commuting with $C$ and annihilating $N$, such that $z b = x b $ for every $b$ in $B$, [a5], [a15]. In other words, the natural morphism $\sigma : I ( B ) \cap C ^ { \prime } \cap N ^ { \perp } \rightarrow M ( B )$ (with $\ker \sigma = B ^ { \perp } \cap C ^ { \prime } \cap N ^ { \perp }$) is surjective. This indicates the size of corona algebras, even compared with large multiplier algebras.
References
| [a1] | Ch.A. Akemann, G.K. Pedersen, "Ideal perturbations of elements in $C ^ { * }$-algebras" Math. Scand. , 41 (1977) pp. 117–139 MR473848 |
| [a2] | Ch.A. Akemann, G.K. Pedersen, J. Tomiyama, "Multipliers of $C ^ { * }$-algebras" J. Funct. Anal. , 13 (1973) pp. 277–301 MR470685 |
| [a3] | B. Blackadar, "Shape theory for $C ^ { * }$-algebras" Math. Scand. , 56 (1985) pp. 249–275 MR813640 |
| [a4] | R.C. Busby, "Double centralizers and extensions of $C ^ { * }$-algebras" Trans. Amer. Math. Soc. , 132 (1968) pp. 79–99 MR225175 |
| [a5] | S. Eilers, T.A. Loring, G.K. Pedersen, "Morphisms of extensions of $C ^ { * }$-algebras: Pushing forward the Busby invariant" Adv. Math. , 147 (1999) pp. 74–109 MR1725815 |
| [a6] | K. Grove, G.K. Pedersen, "Sub-Stonean spaces and corona sets" J. Funct. Anal. , 56 (1984) pp. 124–143 MR0735707 Zbl 0539.54029 |
| [a7] | K. Grove, G.K. Pedersen, "Diagonalizing matrices over $C ( X )$" J. Funct. Anal. , 59 (1984) pp. 65–89 MR0763777 Zbl 0554.46026 |
| [a8] | B.E. Johnson, "An introduction to the theory of centralizers" Proc. London Math. Soc. , 14 (1964) pp. 299–320 MR0159233 Zbl 0143.36102 |
| [a9] | T.A. Loring, "Lifting solutions to perturbing problems in $C ^ { * }$-algebras" , Fields Inst. Monographs , 8 , Amer. Math. Soc. (1997) MR1420863 |
| [a10] | T.A. Loring, G.K. Pedersen, "Projectivity, transitivity and AF telescopes" Trans. Amer. Math. Soc. , 350 (1998) pp. 4313–4339 MR1616003 Zbl 0906.46044 |
| [a11] | C.L. Olsen, G.K. Pedersen, "Corona $C ^ { * }$-algebras and their applications to lifting problems" Math. Scand. , 64 (1989) pp. 63–86 MR1036429 |
| [a12] | G.K. Pedersen, "$C ^ { * }$-algebras and their automorphism groups" , Acad. Press (1979) MR0548006 Zbl 0416.46043 |
| [a13] | G.K. Pedersen, "$S A W ^ { * }$-algebras and corona $C ^ { * }$-algebras, contributions to non-commutative topology" J. Oper. Th. , 4 (1986) pp. 15–32 |
| [a14] | G.K. Pedersen, "The corona construction" J.B. Conway (ed.) B.B. Morrel (ed.) , Proc. 1988 GPOTS-Wabash Conf. , Longman Sci. (1990) pp. 49–92 MR1075635 Zbl 0716.46044 |
| [a15] | G.K. Pedersen, "Extensions of $C ^ { * }$-algebras" S. Doplicher (ed.) et al. (ed.) , Operator Algebras and Quantum Field Theory , Internat. Press, Cambridge, Mass. (1997) pp. 2–35 |
| [a16] | D.C. Taylor, "The strict topology for double centralizer algebras" Trans. Amer. Math. Soc. , 150 (1970) pp. 633–643 MR0290117 Zbl 0204.14701 |
Multipliers-of-C*-algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multipliers-of-C*-algebras&oldid=50820