Multipliers-of-C*-algebras
A 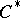 -algebra
-algebra 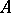 of operators on some Hilbert space
of operators on some Hilbert space 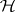 may be viewed as a non-commutative generalization of a function algebra
may be viewed as a non-commutative generalization of a function algebra 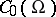 acting as multiplication operators on some
acting as multiplication operators on some 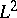 -space associated with a measure on the locally compact space
-space associated with a measure on the locally compact space  . The space
. The space  being compact corresponds naturally to the case where the algebra
being compact corresponds naturally to the case where the algebra 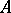 is unital. In the non-unital case any embedding of
is unital. In the non-unital case any embedding of 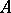 as an essential ideal in some larger unital
as an essential ideal in some larger unital 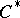 -algebra
-algebra  (i.e., the annihilator of
(i.e., the annihilator of 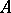 in
in 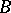 is zero) can be viewed as an analogue of a compactification of the locally compact Hausdorff space
is zero) can be viewed as an analogue of a compactification of the locally compact Hausdorff space  . Thus, the one-point compactification
. Thus, the one-point compactification  of
of  corresponds to the unitization
corresponds to the unitization 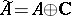 of the algebra
of the algebra 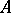 . The analogue of the maximal compactification — the Stone–Čech compactification — is the algebra
. The analogue of the maximal compactification — the Stone–Čech compactification — is the algebra  of multipliers of
of multipliers of 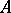 , defined by R.C. Busby in 1967 [a4] and studied in more detail in [a2]. It is defined simply as the idealizer of
, defined by R.C. Busby in 1967 [a4] and studied in more detail in [a2]. It is defined simply as the idealizer of 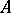 in
in 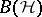 (assuming that
(assuming that 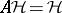 or, equivalently, that no non-zero vector in
or, equivalently, that no non-zero vector in 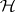 is annihilated by
is annihilated by 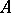 ).
).
Linear operators  and
and 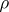 on
on 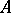 are called left and right centralizers if
are called left and right centralizers if 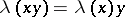 and
and 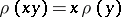 for all
for all  ,
, 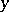 in
in 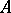 . They are automatically bounded. A double centralizer is a pair
. They are automatically bounded. A double centralizer is a pair  of left, right centralizers such that
of left, right centralizers such that 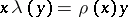 (whence
(whence 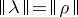 ), and the closed linear spaces of double centralizers becomes a
), and the closed linear spaces of double centralizers becomes a 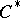 -algebra when product and involution are defined by
-algebra when product and involution are defined by 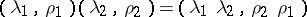 and
and  (where
(where  ). As shown by B.E. Johnson, [a8], there is an isomorphism between the abstractly defined
). As shown by B.E. Johnson, [a8], there is an isomorphism between the abstractly defined  -algebra of double centralizers of
-algebra of double centralizers of  and the concrete
and the concrete 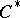 -algebra
-algebra 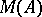 . This, in particular, shows that
. This, in particular, shows that 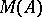 is independent of the given representation of
is independent of the given representation of 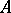 on
on 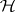 .
.
The strict topology on 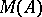 is defined by the semi-norms
is defined by the semi-norms 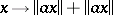 on
on 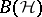 with
with  in
in 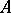 , [a4]. It is used as an analogue of uniform convergence on compact subsets of
, [a4]. It is used as an analogue of uniform convergence on compact subsets of  in function algebras. Thus, it can be shown that
in function algebras. Thus, it can be shown that 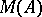 is the strict completion of
is the strict completion of  in
in 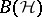 and that the strict dual of
and that the strict dual of 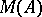 equals the norm dual of
equals the norm dual of  , [a16].
, [a16].
If 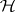 is the universal Hilbert space for
is the universal Hilbert space for 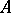 (the orthogonal sum of all Hilbert spaces obtained from states of
(the orthogonal sum of all Hilbert spaces obtained from states of 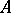 via the Gel'fand–Naimark–Segal construction), then
via the Gel'fand–Naimark–Segal construction), then 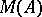 has a more constructive characterization: Let
has a more constructive characterization: Let 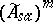 denote the space of self-adjoint operators in
denote the space of self-adjoint operators in 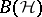 that can be obtained as limits (in the strong topology) of some increasing net of self-adjoint elements from the unitized algebra
that can be obtained as limits (in the strong topology) of some increasing net of self-adjoint elements from the unitized algebra 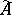 (cf. also Net (directed set); Self-adjoint operator). Similarly, let
(cf. also Net (directed set); Self-adjoint operator). Similarly, let 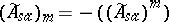 be the space of limits of decreasing nets. Then
be the space of limits of decreasing nets. Then
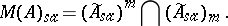 |
Thus, for every self-adjoint multiplier  there are nets
there are nets 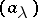 and
and 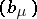 in
in 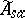 , one increasing, the other decreasing, such that
, one increasing, the other decreasing, such that 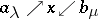 . If
. If 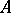 is
is  -unital, i.e. contains a countable approximate unit, in particular if
-unital, i.e. contains a countable approximate unit, in particular if 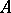 is separable (cf. also Separable algebra), these nets can be taken as sequences, [a2], [a12], p. 12. In the commutative case, where
is separable (cf. also Separable algebra), these nets can be taken as sequences, [a2], [a12], p. 12. In the commutative case, where 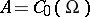 , whence
, whence 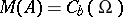 , this expresses the well-known fact that a bounded, real function on
, this expresses the well-known fact that a bounded, real function on  is continuous precisely when it is both lower and upper semi-continuous.
is continuous precisely when it is both lower and upper semi-continuous.
For any  -algebra
-algebra  containing
containing 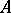 as an ideal there is a natural morphism (i.e. a
as an ideal there is a natural morphism (i.e. a  -homomorphism)
-homomorphism) 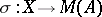 , defined by
, defined by 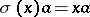 , that extends the identity mapping of
, that extends the identity mapping of 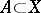 onto
onto 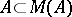 . If
. If 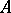 is essential in
is essential in 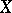 , one therefore obtains an embedding
, one therefore obtains an embedding 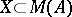 . Any morphism
. Any morphism 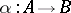 between
between 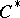 -algebras
-algebras 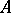 and
and 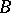 extends uniquely to a strictly continuous morphism
extends uniquely to a strictly continuous morphism  , provided that
, provided that 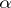 is proper (i.e. maps an approximate unit for
is proper (i.e. maps an approximate unit for 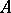 to one for
to one for 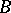 ). Such morphisms are the analogues of proper continuous mappings between locally compact spaces. If
). Such morphisms are the analogues of proper continuous mappings between locally compact spaces. If 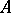 is
is 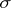 -unital and
-unital and 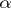 is a quotient morphism, i.e. surjective, then
is a quotient morphism, i.e. surjective, then 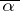 is also surjective. This result may be viewed as a non-commutative generalization of the Tietze extension theorem, [a2], [a13] (cf. also Extension theorems).
is also surjective. This result may be viewed as a non-commutative generalization of the Tietze extension theorem, [a2], [a13] (cf. also Extension theorems).
The corona of a 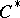 -algebra
-algebra 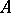 is defined as the quotient
is defined as the quotient 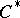 -algebra
-algebra 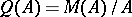 , [a13]. The commutative analogue is the compact Hausdorff space
, [a13]. The commutative analogue is the compact Hausdorff space 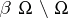 (the corona of the locally compact space
(the corona of the locally compact space  , [a6]), but the pre-eminent example of such algebras is the Calkin algebra
, [a6]), but the pre-eminent example of such algebras is the Calkin algebra 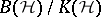 , obtained by taking
, obtained by taking 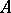 as the algebra
as the algebra  of compact operators on
of compact operators on 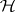 (whence
(whence 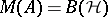 ). Corona
). Corona 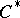 -algebras are usually non-separable and cannot even be represented on separable Hilbert spaces, [a14]. Nevertheless, they have important roles in the formulation of G. Kasparov's KK-theory and the later variation known as E-theory. The foremost application, however, is to the theory of extensions: An extension of
-algebras are usually non-separable and cannot even be represented on separable Hilbert spaces, [a14]. Nevertheless, they have important roles in the formulation of G. Kasparov's KK-theory and the later variation known as E-theory. The foremost application, however, is to the theory of extensions: An extension of 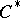 -algebras
-algebras  and
and 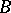 is any
is any 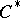 -algebra
-algebra  that fits into a short exact sequence (cf. also Exact sequence)
that fits into a short exact sequence (cf. also Exact sequence)
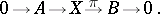 |
Thus, 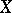 contains
contains 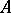 as an ideal, and
as an ideal, and 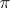 is simply the quotient morphism. In particular,
is simply the quotient morphism. In particular, 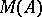 may be regarded as an extension of
may be regarded as an extension of 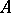 by
by 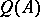 , and in fact a maximal such. Namely, any other extension will give rise to a commutative diagram
, and in fact a maximal such. Namely, any other extension will give rise to a commutative diagram
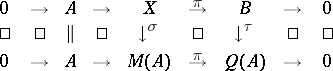 |
Here 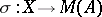 is the morphism defined above and the induced morphism
is the morphism defined above and the induced morphism 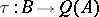 is known as the Busby invariant for
is known as the Busby invariant for 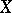 . This invariant determines
. This invariant determines 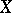 up to an obvious equivalence, because the right square in the diagram above describes
up to an obvious equivalence, because the right square in the diagram above describes 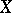 as the pull-back of
as the pull-back of 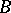 and
and 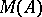 over
over  , i.e.
, i.e.
 |
 |
One therefore has the identification  , [a4], [a5], [a15].
, [a4], [a5], [a15].
For any quotient morphism  between
between 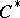 -algebras one may ask whether an element
-algebras one may ask whether an element 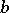 in
in 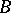 with specific properties is the image of some
with specific properties is the image of some  in
in 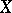 with the same properties. This is known as a lifting problem, and is the non-commutative analogue of extension problems for functions. Many lifting problems have positive (and easy) solutions: If
with the same properties. This is known as a lifting problem, and is the non-commutative analogue of extension problems for functions. Many lifting problems have positive (and easy) solutions: If 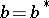 or
or 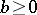 or
or 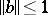 , one can find counter-images in
, one can find counter-images in 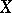 with the same properties. However, the properties
with the same properties. However, the properties 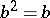 (being idempotent) and
(being idempotent) and  (being normal) are not liftable in general. It follows that the more general commutator relation
(being normal) are not liftable in general. It follows that the more general commutator relation 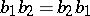 is not liftable either. But the orthogonality relation
is not liftable either. But the orthogonality relation 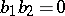 is liftable (even in the
is liftable (even in the  -fold version
-fold version  ). Using this one may show that the nilpotency relation
). Using this one may show that the nilpotency relation 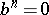 is liftable, [a1], [a11], [a9].
is liftable, [a1], [a11], [a9].
As advocated by T.A. Loring, lifting problems may with advantage be replaced by 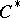 -algebra problems concerning projectivity. A
-algebra problems concerning projectivity. A 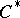 -algebra
-algebra 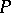 is projective if any morphism
is projective if any morphism 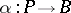 into a quotient
into a quotient 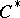 -algebra
-algebra 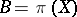 can be factored as
can be factored as 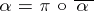 for some morphism
for some morphism 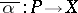 , [a3]. This means that one is lifting a whole
, [a3]. This means that one is lifting a whole 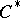 -subalgebra and not just some elements. Projective
-subalgebra and not just some elements. Projective 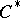 -algebras are the non-commutative analogues of topological spaces that are absolute retracts, but since the category of
-algebras are the non-commutative analogues of topological spaces that are absolute retracts, but since the category of 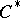 -algebras is vastly larger than the category of locally compact Hausdorff spaces, projectivity is a rare phenomenon. However, the cone over the
-algebras is vastly larger than the category of locally compact Hausdorff spaces, projectivity is a rare phenomenon. However, the cone over the 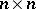 -matrices, i.e. the algebra
-matrices, i.e. the algebra
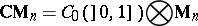 |
is always projective. This means that although matrix units cannot, in general, be lifted from quotients, there are lifts in the "smeared" form given by 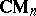 , [a10], [a9].
, [a10], [a9].
Corona  -algebras form an indispensable tool for more complicated lifting problems, because by Busby's theory, mentioned above, it suffices to solve the lifting for quotient morphisms of the form
-algebras form an indispensable tool for more complicated lifting problems, because by Busby's theory, mentioned above, it suffices to solve the lifting for quotient morphisms of the form 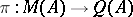 . Thus, one may utilize the special properties that corona algebras have. A brief outline of these follows.
. Thus, one may utilize the special properties that corona algebras have. A brief outline of these follows.
Corona algebras.
In topology, a compact Hausdorff space is called sub-Stonean if any two disjoint, open, 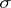 -compact sets have disjoint closures. Exotic as this may sound, it is a property that any corona set
-compact sets have disjoint closures. Exotic as this may sound, it is a property that any corona set 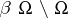 will have, if
will have, if  is locally compact and
is locally compact and 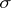 -compact. In such a space, every open,
-compact. In such a space, every open, 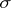 -compact subset is also regularly embedded, i.e. it equals the interior of its closure in
-compact subset is also regularly embedded, i.e. it equals the interior of its closure in 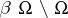 , [a6]. The non-commutative generalization of this is the fact that if
, [a6]. The non-commutative generalization of this is the fact that if 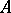 is a
is a 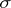 -unital
-unital 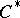 -algebra, then every
-algebra, then every 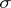 -unital hereditary
-unital hereditary 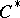 -subalgebra
-subalgebra 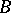 of its corona algebra
of its corona algebra 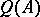 equals its double annihilator, i.e.
equals its double annihilator, i.e. 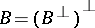 , [a13]. The analogue of the sub–Stonean property, sometimes called the
, [a13]. The analogue of the sub–Stonean property, sometimes called the 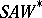 -condition, is even more striking: For any two orthogonal elements
-condition, is even more striking: For any two orthogonal elements  and
and 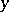 in
in 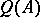 (say
(say 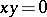 ) there is an element
) there is an element  in
in 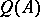 with
with 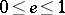 , such that
, such that 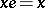 and
and 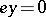 . Even better, if
. Even better, if 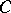 and
and 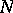 are separable subsets of
are separable subsets of 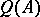 such that
such that  commutes with
commutes with 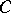 and annihilates
and annihilates 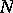 , then the element
, then the element  can be chosen with the same properties, [a11], [a14]. Note that if
can be chosen with the same properties, [a11], [a14]. Note that if  could be taken as a projection, e.g. the range projection of
could be taken as a projection, e.g. the range projection of  , this would be a familiar property in von Neumann algebra theory. The fact that corona algebras will never be von Neumann algebras (if
, this would be a familiar property in von Neumann algebra theory. The fact that corona algebras will never be von Neumann algebras (if 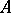 is non-unital and
is non-unital and 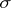 -unital) indicates that the property (first established by G. Kasparov as a "technical lemma" ) is useful. Actually, a potentially stronger version is true: If
-unital) indicates that the property (first established by G. Kasparov as a "technical lemma" ) is useful. Actually, a potentially stronger version is true: If 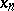 and
and 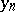 are monotone sequences of self-adjoint elements in
are monotone sequences of self-adjoint elements in 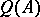 , one increasing, the other decreasing, such that
, one increasing, the other decreasing, such that 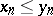 for all
for all  , and if
, and if 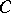 and
and 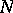 are separable subsets of
are separable subsets of 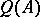 , such that all
, such that all 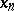 commute with
commute with 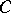 and annihilate
and annihilate 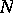 , then there is an element
, then there is an element  in
in 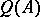 such that
such that 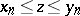 for all
for all  , and
, and  commutes with
commutes with 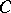 and annihilates
and annihilates 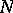 , [a11]. This has as a consequence that if
, [a11]. This has as a consequence that if 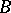 is any
is any 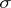 -unital
-unital 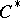 -subalgebra of
-subalgebra of 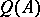 , commuting with
, commuting with 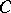 and annihilating
and annihilating 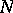 , as above, then for any multiplier
, as above, then for any multiplier  in
in 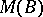 there is an element
there is an element  in the idealizer
in the idealizer 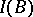 of
of 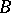 in
in  , still commuting with
, still commuting with 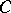 and annihilating
and annihilating 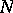 , such that
, such that 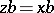 for every
for every 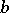 in
in 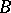 , [a5], [a15]. In other words, the natural morphism
, [a5], [a15]. In other words, the natural morphism 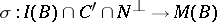 (with
(with 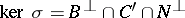 ) is surjective. This indicates the size of corona algebras, even compared with large multiplier algebras.
) is surjective. This indicates the size of corona algebras, even compared with large multiplier algebras.
References
| [a1] | Ch.A. Akemann, G.K. Pedersen, "Ideal perturbations of elements in 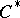 -algebras" Math. Scand. , 41 (1977) pp. 117–139 -algebras" Math. Scand. , 41 (1977) pp. 117–139 |
| [a2] | Ch.A. Akemann, G.K. Pedersen, J. Tomiyama, "Multipliers of 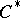 -algebras" J. Funct. Anal. , 13 (1973) pp. 277–301 -algebras" J. Funct. Anal. , 13 (1973) pp. 277–301 |
| [a3] | B. Blackadar, "Shape theory for 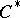 -algebras" Math. Scand. , 56 (1985) pp. 249–275 -algebras" Math. Scand. , 56 (1985) pp. 249–275 |
| [a4] | R.C. Busby, "Double centralizers and extensions of 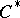 -algebras" Trans. Amer. Math. Soc. , 132 (1968) pp. 79–99 -algebras" Trans. Amer. Math. Soc. , 132 (1968) pp. 79–99 |
| [a5] | S. Eilers, T.A. Loring, G.K. Pedersen, "Morphisms of extensions of 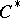 -algebras: Pushing forward the Busby invariant" Adv. Math. , 147 (1999) pp. 74–109 -algebras: Pushing forward the Busby invariant" Adv. Math. , 147 (1999) pp. 74–109 |
| [a6] | K. Grove, G.K. Pedersen, "Sub-Stonean spaces and corona sets" J. Funct. Anal. , 56 (1984) pp. 124–143 |
| [a7] | K. Grove, G.K. Pedersen, "Diagonalizing matrices over 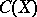 " J. Funct. Anal. , 59 (1984) pp. 65–89 " J. Funct. Anal. , 59 (1984) pp. 65–89 |
| [a8] | B.E. Johnson, "An introduction to the theory of centralizers" Proc. London Math. Soc. , 14 (1964) pp. 299–320 |
| [a9] | T.A. Loring, "Lifting solutions to perturbing problems in 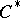 -algebras" , Fields Inst. Monographs , 8 , Amer. Math. Soc. (1997) -algebras" , Fields Inst. Monographs , 8 , Amer. Math. Soc. (1997) |
| [a10] | T.A. Loring, G.K. Pedersen, "Projectivity, transitivity and AF telescopes" Trans. Amer. Math. Soc. , 350 (1998) pp. 4313–4339 |
| [a11] | C.L. Olsen, G.K. Pedersen, "Corona 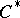 -algebras and their applications to lifting problems" Math. Scand. , 64 (1989) pp. 63–86 -algebras and their applications to lifting problems" Math. Scand. , 64 (1989) pp. 63–86 |
| [a12] | G.K. Pedersen, "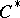 -algebras and their automorphism groups" , Acad. Press (1979) -algebras and their automorphism groups" , Acad. Press (1979) |
| [a13] | G.K. Pedersen, "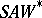 -algebras and corona -algebras and corona 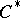 -algebras, contributions to non-commutative topology" J. Oper. Th. , 4 (1986) pp. 15–32 -algebras, contributions to non-commutative topology" J. Oper. Th. , 4 (1986) pp. 15–32 |
| [a14] | G.K. Pedersen, "The corona construction" J.B. Conway (ed.) B.B. Morrel (ed.) , Proc. 1988 GPOTS-Wabash Conf. , Longman Sci. (1990) pp. 49–92 |
| [a15] | G.K. Pedersen, "Extensions of 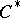 -algebras" S. Doplicher (ed.) et al. (ed.) , Operator Algebras and Quantum Field Theory , Internat. Press, Cambridge, Mass. (1997) pp. 2–35 -algebras" S. Doplicher (ed.) et al. (ed.) , Operator Algebras and Quantum Field Theory , Internat. Press, Cambridge, Mass. (1997) pp. 2–35 |
| [a16] | D.C. Taylor, "The strict topology for double centralizer algebras" Trans. Amer. Math. Soc. , 150 (1970) pp. 633–643 |
Multipliers-of-C*-algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multipliers-of-C*-algebras&oldid=17916