Multiple-correlation coefficient
A measure of the linear dependence between one random variable and a certain collection of random variables. More precisely, if  is a random vector with values in
is a random vector with values in  , then the multiple-correlation coefficient between
, then the multiple-correlation coefficient between  and
and  is defined as the usual correlation coefficient between
is defined as the usual correlation coefficient between  and its best linear approximation
and its best linear approximation  relative to
relative to  , i.e. as its regression relative to
, i.e. as its regression relative to  . The multiple-correlation coefficient has the property that if
. The multiple-correlation coefficient has the property that if  and if
and if
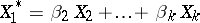 |
is the regression of  relative to
relative to 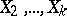 , then among all linear combinations of
, then among all linear combinations of  the variable
the variable  has largest correlation with
has largest correlation with  . In this sense the multiple-correlation coefficient is a special case of the canonical correlation coefficient (cf. Canonical correlation coefficients). For
. In this sense the multiple-correlation coefficient is a special case of the canonical correlation coefficient (cf. Canonical correlation coefficients). For  the multiple-correlation coefficient is the absolute value of the usual correlation coefficient
the multiple-correlation coefficient is the absolute value of the usual correlation coefficient 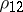 between
between  and
and  . The multiple-correlation coefficient between
. The multiple-correlation coefficient between 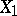 and
and 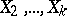 is denoted by
is denoted by 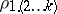 and is expressed in terms of the entries of the correlation matrix
and is expressed in terms of the entries of the correlation matrix  ,
, 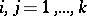 , by
, by
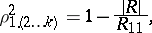 |
where 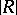 is the determinant of
is the determinant of 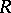 and
and 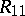 is the cofactor of
is the cofactor of 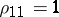 ; here
; here 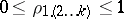 . If
. If  , then, with probability
, then, with probability 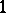 ,
,  is equal to a linear combination of
is equal to a linear combination of  , that is, the joint distribution of
, that is, the joint distribution of 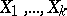 is concentrated on a hyperplane in
is concentrated on a hyperplane in 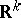 . On the other hand,
. On the other hand,  if and only if
if and only if  , that is, if
, that is, if 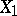 is not correlated with any of
is not correlated with any of 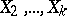 . To calculate the multiple-correlation coefficient one can use the formula
. To calculate the multiple-correlation coefficient one can use the formula
 |
where  is the variance of
is the variance of 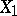 and
and
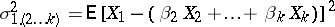 |
is the variance of  with respect to the regression.
with respect to the regression.
The sample analogue of the multiple-correlation coefficient  is
is
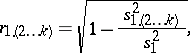 |
where 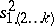 and
and  are estimators of
are estimators of  and
and  based on a sample of size
based on a sample of size  . To test the hypothesis of no relationship, the sampling distribution of
. To test the hypothesis of no relationship, the sampling distribution of 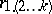 is used. Given that the sample is taken from a multivariate normal distribution, the variable
is used. Given that the sample is taken from a multivariate normal distribution, the variable 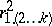 has the beta-distribution with parameters
has the beta-distribution with parameters 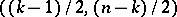 if
if  ; if
; if  , then the distribution of
, then the distribution of  is known, but is somewhat complicated.
is known, but is somewhat complicated.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
Comments
For the distribution of 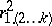 if
if  see [a2], Chapt. 10.
see [a2], Chapt. 10.
References
| [a1] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1958) |
| [a2] | M.L. Eaton, "Multivariate statistics: A vector space approach" , Wiley (1983) |
| [a3] | R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) |
Multiple-correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiple-correlation_coefficient&oldid=12840