Multi-functor
multi-place functor
A function of several arguments, defined on categories, taking values in a category and giving a one-place functor in each argument. More precisely, let  categories
categories 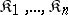 be given. Construct the Cartesian product category
be given. Construct the Cartesian product category 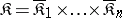 , where each category
, where each category  is either
is either 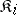 or the opposite category
or the opposite category 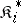 . A one-place covariant functor
. A one-place covariant functor 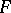 from
from  with values in a category
with values in a category  is called an
is called an  -place functor on
-place functor on 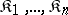 with values in
with values in 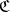 . The functor
. The functor 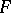 is covariant in those arguments which correspond to the factors
is covariant in those arguments which correspond to the factors 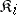 in
in 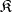 , and contravariant in the remaining arguments.
, and contravariant in the remaining arguments.
The conditions which must be satisfied by a mapping 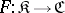 are given below (in the case
are given below (in the case 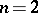 , with the first argument contravariant and the second covariant). The functor
, with the first argument contravariant and the second covariant). The functor 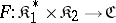 associates to each pair of objects
associates to each pair of objects 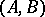 ,
, 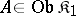 ,
, 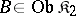 , an object
, an object 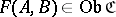 and to each pair of morphisms
and to each pair of morphisms 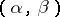 , where
, where
 |
a morphism
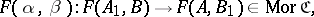 |
in such a way that the following conditions are satisfied:
1) 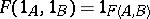 for any pair of objects
for any pair of objects 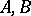 ;
;
2) if 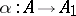 ,
, 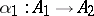 ,
, 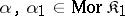 ,
, 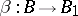 ,
, 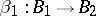 ,
, 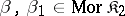 , then
, then
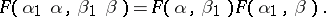 |
Examples of multi-functors.
A) Let 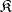 be a category with finite products. Then the product of
be a category with finite products. Then the product of  objects can be considered as an
objects can be considered as an  -place functor that is covariant in all its arguments, defined on
-place functor that is covariant in all its arguments, defined on 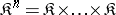 (
( times) and taking values in
times) and taking values in 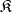 . Similar functors can be constructed for coproducts, etc.
. Similar functors can be constructed for coproducts, etc.
B) Let 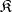 be an arbitrary category. Associate with each pair of objects
be an arbitrary category. Associate with each pair of objects 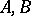 from
from 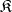 the set of morphisms
the set of morphisms 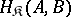 and with each pair of morphism
and with each pair of morphism 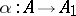 ,
, 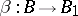 the mapping
the mapping 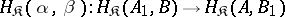 given as follows: if
given as follows: if 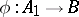 then
then 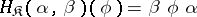 . This construction gives a two-place functor from
. This construction gives a two-place functor from 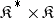 into the category of sets that is contravariant in its first argument and covariant in its second.
into the category of sets that is contravariant in its first argument and covariant in its second.
If 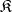 is an additive category, then this functor can be regarded as taking values in the category of Abelian groups.
is an additive category, then this functor can be regarded as taking values in the category of Abelian groups.
C) Let 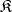 be a category with finite products. Consider the product as a two-place functor
be a category with finite products. Consider the product as a two-place functor 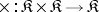 . Then by combining Examples A) and B) it is possible to construct three-place functors
. Then by combining Examples A) and B) it is possible to construct three-place functors 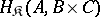 and
and 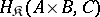 . The first functor is naturally equivalent to the functor
. The first functor is naturally equivalent to the functor 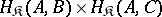 . If
. If  is the category of sets (cf. Sets, category of), the second functor is naturally equivalent to the functor
is the category of sets (cf. Sets, category of), the second functor is naturally equivalent to the functor 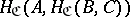 .
.
D) Let 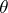 be a small category and let
be a small category and let 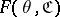 be the category of diagrams over the category of sets
be the category of diagrams over the category of sets 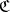 with scheme
with scheme 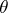 , that is, the category of one-place covariant functors and their natural transformations. A two-place functor
, that is, the category of one-place covariant functors and their natural transformations. A two-place functor 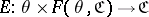 which is covariant in both arguments is constructed as follows: If
which is covariant in both arguments is constructed as follows: If 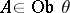 and
and 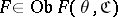 , then
, then 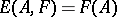 ; if
; if 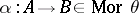 and
and 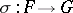 is a natural transformation, then
is a natural transformation, then 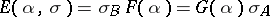 . The functor
. The functor 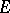 is called the "evaluation functorevaluation functor" . This functor is naturally equivalent to the functor
is called the "evaluation functorevaluation functor" . This functor is naturally equivalent to the functor 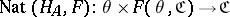 , which associates with an object
, which associates with an object 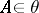 and a functor
and a functor 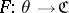 the set of natural transformations of the representable functor
the set of natural transformations of the representable functor 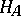 into
into 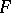 (Yoneda's lemma).
(Yoneda's lemma).
Comments
A two-place functor is often called a bifunctor.
References
| [a1] | B. Mitchell, "Theory of categories" , Acad. Press (1965) |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
Multi-functor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-functor&oldid=18045