Movable space
A compact space  , embedded in the Hilbert cube
, embedded in the Hilbert cube  , is movable provided every neighbourhood
, is movable provided every neighbourhood  of
of  in
in  admits a neighbourhood
admits a neighbourhood  of
of  such that, for any other neighbourhood
such that, for any other neighbourhood  of
of  , there exists a homotopy
, there exists a homotopy 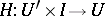 with
with 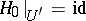 ,
, 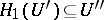 . In other words, sufficiently small neighbourhoods of
. In other words, sufficiently small neighbourhoods of 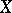 can be deformed arbitrarily close to
can be deformed arbitrarily close to 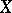 [a2]. K. Borsuk proved that movability is a shape invariant. The solenoids (cf. Solenoid) are examples of non-movable continua.
[a2]. K. Borsuk proved that movability is a shape invariant. The solenoids (cf. Solenoid) are examples of non-movable continua.
The question whether movable continua are always pointed movable is still (1998) open.
For movable spaces various shape-theoretic results assume simpler form. E.g., if 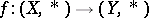 is a pointed shape morphism between pointed movable metric continua (cf. also Pointed space; Continuum; Shape theory), which induces isomorphisms of the shape groups
is a pointed shape morphism between pointed movable metric continua (cf. also Pointed space; Continuum; Shape theory), which induces isomorphisms of the shape groups 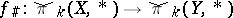 , for all
, for all 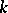 and if the spaces
and if the spaces 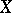 ,
, 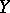 are finite-dimensional, then
are finite-dimensional, then 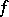 is a pointed shape equivalence. This is a consequence of the shape-theoretic Whitehead theorem (cf. also Homotopy type; Homotopy group) and the fact that such an
is a pointed shape equivalence. This is a consequence of the shape-theoretic Whitehead theorem (cf. also Homotopy type; Homotopy group) and the fact that such an 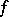 induces isomorphisms of homotopy pro-groups
induces isomorphisms of homotopy pro-groups 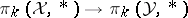 [a6], [a5].
[a6], [a5].
Borsuk also introduced the notion of  -movability. A compactum
-movability. A compactum  is
is  -movable provided every neighbourhood
-movable provided every neighbourhood  of
of 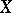 in
in 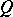 admits a neighbourhood
admits a neighbourhood 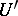 of
of 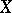 in
in 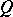 such that, for any neighbourhood
such that, for any neighbourhood 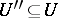 of
of 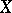 , any compactum
, any compactum 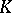 of dimension
of dimension 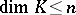 and any mapping
and any mapping 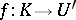 , there exists a mapping
, there exists a mapping 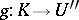 such that
such that 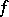 and
and 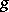 are homotopic in
are homotopic in 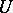 . Clearly, if a compactum
. Clearly, if a compactum 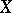 is
is  -movable and
-movable and 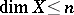 , then
, then 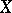 is movable. Moreover, every
is movable. Moreover, every 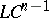 -compactum is
-compactum is  -movable [a3]. The notion of
-movable [a3]. The notion of  -movability was the beginning of the
-movability was the beginning of the  -shape theory, which was especially developed by A.Ch. Chigogidze [a4] (cf. also Shape theory). The
-shape theory, which was especially developed by A.Ch. Chigogidze [a4] (cf. also Shape theory). The  -shape theory is an important tool in the theory of
-shape theory is an important tool in the theory of  -dimensional Menger manifolds, developed by M. Bestvina [a1].
-dimensional Menger manifolds, developed by M. Bestvina [a1].
References
| [a1] | M. Bestvina, "Characterizing 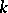 -dimensional universal Menger compacta" Memoirs Amer. Math. Soc. , 71 : 380 (1988) pp. 1–110 -dimensional universal Menger compacta" Memoirs Amer. Math. Soc. , 71 : 380 (1988) pp. 1–110 |
| [a2] | K. Borsuk, "On movable compacta" Fund. Math. , 66 (1969) pp. 137–146 |
| [a3] | K. Borsuk, "On the  -movability" Bull. Acad. Polon. Sci. Ser. Sci. Math. Astr. Phys. , 20 (1972) pp. 859–864 -movability" Bull. Acad. Polon. Sci. Ser. Sci. Math. Astr. Phys. , 20 (1972) pp. 859–864 |
| [a4] | A.Ch. Chigogidze, "Theory of  -shape" Uspekhi Mat. Nauk , 44 : 5 (1989) pp. 117–140 (In Russian) -shape" Uspekhi Mat. Nauk , 44 : 5 (1989) pp. 117–140 (In Russian) |
| [a5] | J. Dydak, "The Whitehead and the Smale theorems in shape theory" Dissert. Math. , 156 (1979) pp. 1–55 |
| [a6] | J.E. Keesling, "On the Whitehead theorem in shape theory" Fund. Math. , 92 (1976) pp. 247–253 |
Movable space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Movable_space&oldid=18351