Moulding surface
A surface generated by the orthogonal trajectories of a one-parameter family of planes. Moulding surfaces have one family of planar lines of curvature that are simultaneously geodesics for the moulding surface. If the family of planes is degenerated into a bundle, then the moulding surface will be a surface of revolution. The sections of a moulding surface by planes of the family are called meridians, and the orthogonal trajectories are called parallels of the moulding surface. All meridians are congruent, so that a moulding surface can be formed by the motion of a planar line  (the meridian), the plane of which moves without sliding along a certain developable surface. This surface is called the directing surface of the moulding surface and is one of the sheets of its evolute. If
(the meridian), the plane of which moves without sliding along a certain developable surface. This surface is called the directing surface of the moulding surface and is one of the sheets of its evolute. If 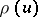 is the position vector of one parallel position, then the position vector of the moulding surface will be
is the position vector of one parallel position, then the position vector of the moulding surface will be
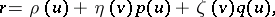 |
where 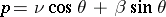 ,
, 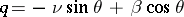 ,
,  is the principal normal,
is the principal normal, 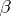 is the binormal,
is the binormal,  is the torsion of the curve
is the torsion of the curve 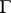 , and
, and 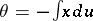 . Its line element is given by:
. Its line element is given by:
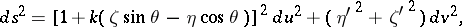 |
where 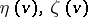 are the equations of
are the equations of 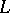 and
and 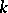 is the curvature of
is the curvature of 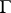 .
.
Comments
References
| [a1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Chelsea, reprint (1972) pp. Sects. 85–87 |
Moulding surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moulding_surface&oldid=19030