Motzkin transposition theorem
The thesis of T.S. Motzkin, [a6], in particular his transposition theorem, was a milestone in the development of linear inequalities and related areas.
For two vectors 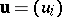 and
and 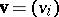 of equal dimension one denotes by
of equal dimension one denotes by 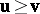 and
and 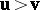 that the indicated inequality holds componentwise, and by
that the indicated inequality holds componentwise, and by 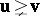 the fact
the fact 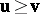 and
and  .
.
Systems of linear inequalities appear in several forms; the following examples are typical:
a) 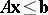 ;
;
b) 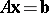 ,
, 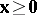 ;
;
c) 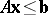 ,
,  ;
;
d) 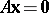 ,
, 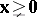 ;
;
e) 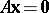 ,
, 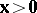 ;
;
f) 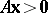 ,
, 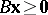 ,
, 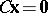 .
.
In each of these so-called primal systems the existence of solutions is characterized by means of a dual system, using the transposes of matrices in the primal system. Hence the name "transposition theorem" . The relation between the primal and dual systems is sometimes given as a "theorem of alternatives" , listing alternatives, i.e. statements 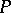 ,
, 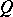 satisfying
satisfying 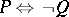 (where
(where  denotes negation), in words: either
denotes negation), in words: either 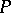 or
or 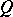 but never both.
but never both.
Relations between a)–f).
a) and b) are equivalent representations. Indeed, they can be written as
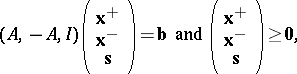 |
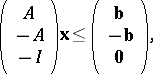 |
respectively.
The remaining systems involve strict inequalities or non-trivial solutions. For example, d) and e) concern the existence of non-trivial solutions and positive solutions, respectively, for the system
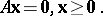 |
Taking 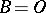 and
and 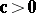 in c) gives a), showing that a) and b) are special cases of c). Similarly, the systems d) and e) are special cases of f), which itself is a special case of c) with
in c) gives a), showing that a) and b) are special cases of c). Similarly, the systems d) and e) are special cases of f), which itself is a special case of c) with 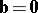 ,
, 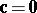 . In fact, every system of linear inequalities can be written as c).
. In fact, every system of linear inequalities can be written as c).
The following two versions of Motzkin's transposition theorem, [a6], concern systems c) and f):
(solvability of c)) Given matrices 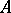 ,
, 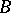 and vectors
and vectors 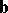 ,
,  , the following are equivalent:
, the following are equivalent:
c1) the system 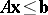 ,
, 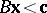 has a solution
has a solution  ;
;
c2) for all vectors 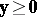 ,
, 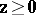 ,
,
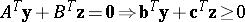 |
and
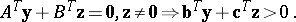 |
(solvability of f)) Let 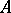 ,
, 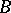 ,
, 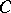 be given matrices, with
be given matrices, with 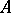 non-vacuous. Then the following are alternatives:
non-vacuous. Then the following are alternatives:
f1) 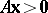 ,
, 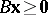 ,
, 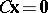 has a solution
has a solution  ;
;
f2) 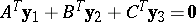 ,
, 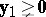 ,
, 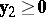 has solutions
has solutions 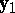 ,
,  ,
, 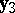 .
.
Special cases of Motzkin's theorem include the following theorems.
Farkas theorem.
(See also [a2].) Let 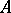 be a given matrix and
be a given matrix and 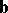 a given vector.
a given vector.
Farkas' theorem for system a) says that the following are equivalent:
a1) the system 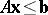 has a solution
has a solution  ;
;
a2) 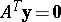 ,
, 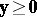
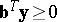 .
.
Farkas' theorem for system b) says that the following are equivalent:
b1) the system 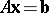 ,
, 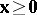 has a solution
has a solution  ;
;
b2) 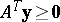
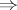
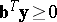 .
.
The positively homogeneous systems d) and e) are covered by the following two theorems.
Gordan's theorem.
(See also [a3].) Given a matrix  , the following are alternatives:
, the following are alternatives:
d1) 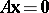 ,
,  has a solution
has a solution  ;
;
d2)  has a solution
has a solution 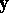 .
.
Stiemke's theorem.
(See also [a9].) Given a matrix 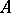 , the following are alternatives:
, the following are alternatives:
e1)  ,
, 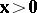 has a solution
has a solution  ;
;
e2) 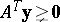 has a solution
has a solution 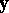 .
.
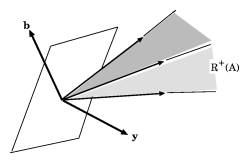
Figure: m130240a
A hyperplane with normal  separating
separating  and
and 
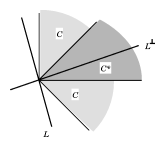
Figure: m130240b
Illustration of the alternatives (a6):  ,
, 
Separation theorems.
The above results are separation theorems, or statements about the existence of hyperplanes separating certain disjoint convex sets. First, some terminology. A set 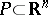 is polyhedral (and necessarily convex) if it is the intersection of finitely many closed half-spaces, say
is polyhedral (and necessarily convex) if it is the intersection of finitely many closed half-spaces, say
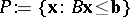 | (a1) |
 |
A finitely generated cone is the set of non-negative linear combinations of finitely many vectors (generators). An example is the cone generated by the columns of a matrix  :
:
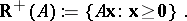 | (a2) |
The dual (or polar)  of a non-empty set
of a non-empty set  is defined as
is defined as
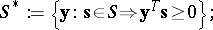 | (a3) |
it is a closed convex cone. In particular,
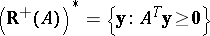 | (a4) |
is a polyhedral cone. Farkas' theorem b1) states that the vector  is in the cone
is in the cone 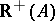 . The equivalent statement b2) says that
. The equivalent statement b2) says that 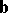 cannot be separated from
cannot be separated from 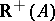 by a hyperplane: such a separating hyperplane would have a normal
by a hyperplane: such a separating hyperplane would have a normal 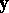 satisfying
satisfying
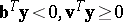 |
for all 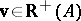 (see e.g. Fig.a1), which by (a4) is a negation of b2). Farkas' theorem for system b) states that for any matrix
(see e.g. Fig.a1), which by (a4) is a negation of b2). Farkas' theorem for system b) states that for any matrix  ,
,
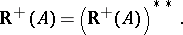 | (a5) |
In general, a set 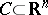 is a closed convex cone if and only if
is a closed convex cone if and only if  . Farkas' theorem for system b) also implies that a cone in
. Farkas' theorem for system b) also implies that a cone in 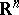 is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [a8], Corol. 7.1a). More generally, a set
is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [a8], Corol. 7.1a). More generally, a set 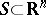 is polyhedral if and only if it is the sum of a finitely generated cone and the convex hull of finitely many points (the Minkowski–Steinitz–Weyl theorem, [a8], Corol. 7.1b).
is polyhedral if and only if it is the sum of a finitely generated cone and the convex hull of finitely many points (the Minkowski–Steinitz–Weyl theorem, [a8], Corol. 7.1b).
The theorems of Stiemke and Gordan can be interpreted as geometric statements about intersections 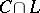 of a pointed closed convex cone
of a pointed closed convex cone 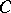 and a subspace
and a subspace 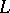 in
in  . Let
. Let 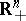 denote the non-negative orthant in
denote the non-negative orthant in 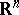 .
.
Thus, Gordan' theorem d1) says that 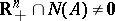 , where
, where 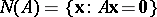 is the null space of
is the null space of  . And Stiemke's theorem e1) says that
. And Stiemke's theorem e1) says that 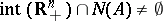 , where
, where 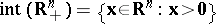 .
.
In each case, the dual system uses the intersection 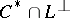 , where
, where 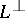 is the orthogonal complement of
is the orthogonal complement of 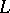 . For example, the statements
. For example, the statements
 | (a6) |
are mutually exclusive (see e.g. Fig.a2), for otherwise
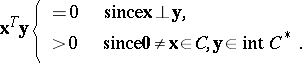 |
To make the statements in (a6) alternatives, one has to show that one of them occurs, the hard part of the proof. Returning to the theorems of Gordan and Stiemke, recall that 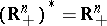 and
and 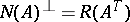 . Then Gordan's theorem d1),
. Then Gordan's theorem d1), 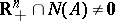 , and d2),
, and d2), 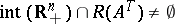 , are alternatives.
, are alternatives.
Likewise, Stiemke's theorems e1), 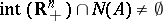 , and e2),
, and e2),  , are alternatives.
, are alternatives.
For history, see [a8], pp. 209–228. For theorems of alternatives, see [a5], pp. 27–37. Generalizations can be found in [a10], [a1], [a11], Sec. 21–22, especially Thm. 21.1; 22.6. Finally, see [a7], [a5], p.100, for applications.
References
| [a1] | K. Fan, "Systems of linear inequalities" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956,}) pp. 99–156 |
| [a2] | J. Farkas, "Über die Theorie der einfachen Ungleichungen" J. Reine Angew. Math. , 124 (1902) pp. 1–24 |
| [a3] | P. Gordan, "Über die Auflösungen linearer Gleighungen mit reelen Coefficienten" Math. Ann. , 6 (1873) pp. 23–28 |
| [a4] | "Linear inequalities and related systems" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956) |
| [a5] | O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969) |
| [a6] | T.S. Motzkin, "Beiträge zur Theorie der linearen Ungleichungen" Inaugural Diss. (Basel, Jerusalem) (1936) |
| [a7] | T.S. Motzkin, "Two consequences of the transposition theorem on linear inequalities" Econometrica , 19 (1951) pp. 184–185 |
| [a8] | A. Schrijver, "Theory of linear and integer programming" , Wiley/Interscience (1986) |
| [a9] | E. Stiemke, "Über positive Lösungen homogener linearer Gleichungen" Math. Ann. , 76 (1915) pp. 340–342 |
| [a10] | A.W. Tucker, "Dual systems of homogeneous linear relations" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956) pp. 3–18 |
| [a11] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) |
Motzkin transposition theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Motzkin_transposition_theorem&oldid=14730