Difference between revisions of "Morse theory"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | m0650101.png | ||
| + | $#A+1 = 214 n = 1 | ||
| + | $#C+1 = 214 : ~/encyclopedia/old_files/data/M065/M.0605010 Morse theory | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The common name for three different theories based on ideas of M. Morse [[#References|[1]]] and describing the relation between algebraic-topological properties of topological spaces and extremal properties of functions (functionals) on them. Morse theory is a branch of [[Variational calculus in the large|variational calculus in the large]] (calculus of variations in the large); however, the latter is broader: for example, it includes the theory of categories (cf. [[Category (in the sense of Lyusternik–Shnirel'man)|Category (in the sense of Lyusternik–Shnirel'man)]]). | The common name for three different theories based on ideas of M. Morse [[#References|[1]]] and describing the relation between algebraic-topological properties of topological spaces and extremal properties of functions (functionals) on them. Morse theory is a branch of [[Variational calculus in the large|variational calculus in the large]] (calculus of variations in the large); however, the latter is broader: for example, it includes the theory of categories (cf. [[Category (in the sense of Lyusternik–Shnirel'man)|Category (in the sense of Lyusternik–Shnirel'man)]]). | ||
| − | 1) Morse theory of critical points (cf. [[Critical point|Critical point]]) of smooth functions | + | 1) Morse theory of critical points (cf. [[Critical point|Critical point]]) of smooth functions $ f $ |
| + | on a smooth manifold $ M $( | ||
| + | briefly, Morse theory 1) is divided into two parts: local and global. The local part is related to the idea of a critical point of a smooth function, the [[Hessian of a function|Hessian of a function]] at its critical point, the [[Morse index|Morse index]] of a critical point, etc. The basic result is the [[Morse lemma|Morse lemma]], which describes the structure of a smooth function in a neighbourhood of a non-degenerate critical point. | ||
The study of smooth functions in neighbourhoods of degenerate points does not properly belong to Morse theory, it does rather belong to the separate theory of [[Singularities of differentiable mappings|singularities of differentiable mappings]]. | The study of smooth functions in neighbourhoods of degenerate points does not properly belong to Morse theory, it does rather belong to the separate theory of [[Singularities of differentiable mappings|singularities of differentiable mappings]]. | ||
| − | The basic results in global Morse theory are as follows. Let | + | The basic results in global Morse theory are as follows. Let $ f $ |
| + | be a function on a smooth manifold $ M $. | ||
| + | If the set $ f ^ { - 1 } ( a) $ | ||
| + | does not contain a critical point of $ f $ | ||
| + | and does not intersect the boundary of $ M $, | ||
| + | then $ M ^ {a} = f ^ { - 1 } ( - \infty , a) $ | ||
| + | is a smooth manifold with boundary $ f ^ { - 1 } ( a) $. | ||
| + | If the set $ f ^ { - 1 } [ a , b ] $ | ||
| + | is compact, does not intersect the boundary of $ M $ | ||
| + | and does not contain a critical point of $ f $, | ||
| + | then there is a smooth isotopy $ h _ {t} : M \rightarrow M $, | ||
| + | $ 0 \leq t \leq 1 $( | ||
| + | realized by shifting along the trajectories of the gradient of $ f $), | ||
| + | such that $ h _ {0} = \mathop{\rm id} _ {M} $ | ||
| + | and $ h _ {1} $ | ||
| + | diffeomorphically maps $ M ^ {b} $ | ||
| + | onto $ M ^ {a} $. | ||
| + | In particular, $ M ^ {b} $ | ||
| + | is diffeomorphic to $ M ^ {a} $ | ||
| + | and the inclusion $ M ^ {a} \subset M ^ {b} $ | ||
| + | is a homotopy equivalence. | ||
| − | If | + | If $ f ^ { - 1 } [ a , b ] $ |
| + | is compact, does not intersect the boundary of $ M $ | ||
| + | and contains precisely one critical point $ p \in f ^ { - 1 } ( a , b ) $ | ||
| + | with Morse index $ \lambda $, | ||
| + | then $ M ^ {b} $ | ||
| + | is diffeomorphic to a manifold obtained from $ M ^ {a} $ | ||
| + | by glueing a handle of index $ \lambda $( | ||
| + | see [[Morse surgery|Morse surgery]]). In particular, if $ p $ | ||
| + | is the unique global minimum point of $ f $, | ||
| + | then for small $ \epsilon > 0 $ | ||
| + | the set $ M ^ { f ( p) + \epsilon } $ | ||
| + | is diffeomorphic to the disc $ D ^ {n} $, | ||
| + | where $ n = \mathop{\rm dim} M $. | ||
| + | Hence it follows that if $ M $ | ||
| + | is a closed smooth manifold having a function with precisely two critical points (both non-degenerate), then $ M $ | ||
| + | is obtained by glueing two smooth discs along their common boundary and, therefore, it is homeomorphic (but in general not diffeomorphic) to the sphere $ S ^ {n} $. | ||
| − | Since glueing a handle of index | + | Since glueing a handle of index $ \lambda $ |
| + | is homotopically equivalent to glueing a cell of dimension $ \lambda $, | ||
| + | the following fundamental theorem of Morse theory 1 follows immediately: Corresponding to each [[Morse function|Morse function]] $ f $ | ||
| + | on a smooth manifold $ M $( | ||
| + | without boundary) is a [[CW-complex|CW-complex]] homotopically equivalent to $ M $; | ||
| + | its cells are in bijective correspondence with the critical points of $ f $ | ||
| + | and the dimension of a cell is equal to the index of the corresponding critical point. The [[Morse inequalities|Morse inequalities]] are an immediate consequence of this theorem. An analogous theorem is valid for a Morse function on a triple $ ( W ; V _ {0} , V _ {1} ) $. | ||
| − | 2) Morse theory of geodesics on a Riemannian manifold (briefly, Morse theory 2) describes the homotopy type of the [[Loop space|loop space]] | + | 2) Morse theory of geodesics on a Riemannian manifold (briefly, Morse theory 2) describes the homotopy type of the [[Loop space|loop space]] $ \Omega M $ |
| + | of a smooth manifold $ M $ | ||
| + | with a Riemannian metric $ g _ {ij} $. | ||
| + | Its aim is to transfer the results of Morse theory 1 to this space (more correctly, to a suitable model of it). The role of $ f $ | ||
| + | is played here by an action functional $ E $( | ||
| + | sometimes called energy functional, [[#References|[5]]]), defined on the space $ \mathop{\rm PS} ( M) $ | ||
| + | of piecewise-smooth paths $ \omega : t \rightarrow \omega ( t) $, | ||
| + | $ 0 \leq t \leq 1 $, | ||
| + | whose value on a path $ \omega \in \mathop{\rm PS} ( M) $ | ||
| + | is defined, in local coordinates $ x ^ {1} \dots x ^ {n} $, | ||
| + | by the formula | ||
| − | + | $$ | |
| + | E ( \omega ) = \ | ||
| + | \int\limits _ { 0 } ^ { 1 } | ||
| + | g _ {ij} d x ^ {i} d x ^ {j} . | ||
| + | $$ | ||
In the initial construction of Morse theory the length functional | In the initial construction of Morse theory the length functional | ||
| − | + | $$ | |
| + | L ( \omega ) = \ | ||
| + | \int\limits _ { 0 } ^ { 1 } | ||
| + | \sqrt {g _ {ij} d x ^ {i} d x ^ {j} } | ||
| + | $$ | ||
| − | was considered, but for many technical reasons | + | was considered, but for many technical reasons $ E $ |
| + | turned out to be preferable. At the same time the extremals of $ E $( | ||
| + | that is, paths $ \omega \in \mathop{\rm PS} ( M) $ | ||
| + | for which the linear functional $ E _ {*} $ | ||
| + | defined by the variation $ \delta E $ | ||
| + | of $ E $ | ||
| + | is zero on $ T _ \omega $) | ||
| + | coincide with the geodesics of the metric $ g _ {ij} $( | ||
| + | the extremals of the functional $ L $) | ||
| + | in their natural parametrization. | ||
| − | Let | + | Let $ p $ |
| + | and $ q $ | ||
| + | be two (not necessarily distinct) points of $ M $, | ||
| + | and let $ \Omega ^ { \mathop{\rm PS} } ( M ; p , q ) \subset \mathop{\rm PS} ( M) $ | ||
| + | be the space of piecewise-smooth paths joining $ p $ | ||
| + | to $ q $. | ||
| + | For each $ l \in \mathbf R $, | ||
| + | put | ||
| − | + | $$ | |
| + | \Omega _ {l} = \ | ||
| + | \Omega _ {l} ^ { \mathop{\rm PS} } | ||
| + | ( M ; p , q ) = E ^ {-} 1 [ 0 , l ] \cap \Omega ^ { | ||
| + | \mathop{\rm PS} } | ||
| + | ( M ; p , q ) . | ||
| + | $$ | ||
| − | If | + | If $ M $ |
| + | is complete, then $ \Omega _ {l} ^ {0} = E ^ {-} 1 [ 0 , l ) \cap \Omega _ {l} $( | ||
| + | the interior of $ \Omega _ {l} $) | ||
| + | is a [[Deformation retract|deformation retract]] of a smooth manifold $ B $ | ||
| + | whose points are "polygonal geodesics" with a fixed number of links, joining $ p $ | ||
| + | to $ q $( | ||
| + | so that, in particular, $ B $ | ||
| + | contains all geodesics from $ \Omega _ {l} ^ {0} $). | ||
| + | Here $ E ^ \prime = E \mid _ {B} : B \rightarrow \mathbf R $ | ||
| + | is a smooth function; for any $ a < l $ | ||
| + | the set $ B ^ {a} = ( E ^ \prime ) ^ {-} 1 [ 0 , a ] $ | ||
| + | is compact and is a deformation retract of $ \Omega _ {a} $; | ||
| + | the critical points of $ E ^ \prime $ | ||
| + | coincide with the extremals of the functional $ E : \Omega _ {l} ^ {0} \rightarrow \mathbf R $ | ||
| + | and are geodesics of length $ < \sqrt l $ | ||
| + | joining $ p $ | ||
| + | and $ q $; | ||
| + | the Morse indices of the critical points of $ E ^ \prime $ | ||
| + | are equal to the Morse indices of the corresponding geodesics; the null space $ N _ \gamma $ | ||
| + | of $ E _ {**} $ | ||
| + | on a geodesic $ \gamma \in \Omega _ {l} ^ {0} $ | ||
| + | is finite dimensional and isomorphic to the null space of the Hessian of $ E ^ \prime $ | ||
| + | at the corresponding critical point; in particular, if $ p $ | ||
| + | and $ q $ | ||
| + | are not conjugate on any geodesic $ \gamma $ | ||
| + | joining them, then $ E ^ \prime $ | ||
| + | is a Morse function. Applying Morse theory 1, passing to the limit as $ l \rightarrow \infty $ | ||
| + | and noting that $ \Omega ^ { \mathop{\rm PS} } ( M ; p , q ) $ | ||
| + | is homotopically equivalent to the space $ \Omega ( M ; p , q ) $ | ||
| + | of all continuous paths joining $ p $ | ||
| + | to $ q $, | ||
| + | one obtains the following fundamental theorem of Morse theory 2: Let $ M $ | ||
| + | be a complete Riemannian manifold and let $ p $ | ||
| + | and $ q $ | ||
| + | be two points not conjugate on any geodesic joining them. The space $ \Omega ( M ; p , q ) $ | ||
| + | of all paths joining $ p $ | ||
| + | and $ q $ | ||
| + | is homotopically equivalent to a CW-complex all cells of dimension $ \lambda $ | ||
| + | of which are in bijective correspondence with the geodesics of index $ \lambda $ | ||
| + | joining $ p $ | ||
| + | to $ q $. | ||
| + | Since the homotopy type of $ \Omega ( M ; p , q ) $ | ||
| + | does not depend on the choice of $ p $ | ||
| + | and $ q $, | ||
| + | this theorem gives, in particular, a description of the homotopy type of the loop space $ \Omega M $. | ||
It is known | It is known | ||
| − | that for a non-contractible manifold | + | that for a non-contractible manifold $ M $ |
| + | the space $ \Omega M $ | ||
| + | has non-trivial homology groups in arbitrarily high dimension. By the fundamental theorem of Morse theory 2 it follows that non-conjugate points in a complete Riemannian non-contractible manifold are joined by infinitely many geodesics (by the example of the sphere it is clear, in general, that these geodesics may be segments of one periodic geodesic). | ||
| − | In the description of the homotopy type given by the fundamental theorem, Jacobi fields (cf. [[Jacobi equation|Jacobi equation]] and [[Jacobi vector field|Jacobi vector field]]) (implicitly) appear, therefore Morse theory establishes a connection between the curvature of a manifold and its topology. For example, if | + | In the description of the homotopy type given by the fundamental theorem, Jacobi fields (cf. [[Jacobi equation|Jacobi equation]] and [[Jacobi vector field|Jacobi vector field]]) (implicitly) appear, therefore Morse theory establishes a connection between the curvature of a manifold and its topology. For example, if $ M $ |
| + | is a complete simply-connected Riemannian manifold of non-positive curvature in all two-dimensional directions, then any Jacobi field vanishing at two points of a geodesic is identically zero. Therefore the loop space $ \Omega M $ | ||
| + | of such a manifold has the type of a zero-dimensional CW-complex, and consequently (in view of the simple connectedness of $ M $) | ||
| + | is contractible. Therefore $ M $ | ||
| + | is contractible, that is, is homotopically equivalent to $ \mathbf R ^ {n} $. | ||
| + | A more precise use of Morse theory shows that $ M $ | ||
| + | is even diffeomorphic to $ \mathbf R ^ {n} $( | ||
| + | see [[#References|[3]]], [[#References|[5]]]). | ||
| − | The application of Morse theory to the topology of Lie groups has turned out to be very effective [[#References|[2]]]. For example, for any simply-connected Lie group | + | The application of Morse theory to the topology of Lie groups has turned out to be very effective [[#References|[2]]]. For example, for any simply-connected Lie group $ G $ |
| + | the space $ \Omega G $ | ||
| + | has the homotopy type of a CW-complex with only odd-dimensional cells. The apotheosis here is the [[Bott periodicity theorem|Bott periodicity theorem]], which plays a fundamental role in $ K $- | ||
| + | theory and, consequently, in the whole of differential topology. Let $ U $ | ||
| + | be the limit of the sequence of nested unitary groups $ \dots \subset U _ {n} \subset U _ {n+} 1 \subset \dots $ | ||
| + | and let $ O $ | ||
| + | be the limit of the sequence of nested orthogonal groups $ \dots \subset O _ {n} \subset O _ {n+} 1 \subset \dots $. | ||
| + | Bott's periodicity theorem asserts that there are homotopy equivalences $ \Omega ^ {2} U \sim U $, | ||
| + | $ \Omega ^ {8} O \sim O $, | ||
| + | where $ \Omega ^ {n} $ | ||
| + | is the $ n $- | ||
| + | th iterate of the functor of passing to the loop space. This theorem allows one to calculate the homotopy groups $ \pi _ {i} U $ | ||
| + | and $ \pi _ {i} O $ | ||
| + | and, consequently, the homotopy groups $ \pi _ {i} U _ {n} $ | ||
| + | and $ \pi _ {j} O _ {n} $ | ||
| + | for $ i < 2 n $, | ||
| + | $ j < n $. | ||
| − | More theory 2 generalizes also to the case when instead of points | + | More theory 2 generalizes also to the case when instead of points $ p , q $ |
| + | smooth submanifolds $ V _ {0} , V _ {1} $ | ||
| + | of $ M $ | ||
| + | are considered. The action functional is studied on the space $ \Omega ^ { \mathop{\rm PS} } ( M ; V _ {0} , V _ {1} ) $ | ||
| + | of all piecewise-smooth paths $ \omega : t \rightarrow \omega ( t) $, | ||
| + | $ 0 \leq t \leq 1 $, | ||
| + | $ \omega ( i) \in V _ {i} $, | ||
| + | $ i = 0 , 1 $, | ||
| + | that are transversal at the end-points to $ V _ {0} $ | ||
| + | and $ V _ {1} $, | ||
| + | and a relation between the extremals of this functional and the homotopy type of $ \Omega ( M ; V _ {0} , V _ {1} ) $ | ||
| + | has been established. The corresponding fundamental theorem is analogous to the above-mentioned fundamental theorem of Morse theory 2; the difficulty is in the geometric interpretation of the Morse index of a geodesic. | ||
| − | 3) The natural development of Morse theory 2 is Morse theory for critical points of smooth functions on Banach (infinite-dimensional) manifolds — Morse theory 3, which is no longer an analogue, but a direct generalization of Morse theory 1. At present (1989) Morse theory 3 is at an initial stage and has been constructed only in a very preliminary context under very strong (and clearly not necessary) conditions on the model Banach space (on separable- and Hilbert-type spaces), when no specifically functional-analytic difficulties arise [[#References|[9]]], although there have been attempts at a construction of Morse theory 3 in fairly general situations. Therefore, in its modern form, Morse theory 3 is an almost verbatim re-iteration of Morse theory 1. The only difference worth mentioning is that in Morse theory 3 the compactness of | + | 3) The natural development of Morse theory 2 is Morse theory for critical points of smooth functions on Banach (infinite-dimensional) manifolds — Morse theory 3, which is no longer an analogue, but a direct generalization of Morse theory 1. At present (1989) Morse theory 3 is at an initial stage and has been constructed only in a very preliminary context under very strong (and clearly not necessary) conditions on the model Banach space (on separable- and Hilbert-type spaces), when no specifically functional-analytic difficulties arise [[#References|[9]]], although there have been attempts at a construction of Morse theory 3 in fairly general situations. Therefore, in its modern form, Morse theory 3 is an almost verbatim re-iteration of Morse theory 1. The only difference worth mentioning is that in Morse theory 3 the compactness of $ f ^ { - 1 } [ a , b ] $ |
| + | is replaced by condition $ C $ | ||
| + | of Palais–Smale (see [[Morse function|Morse function]]), which, besides, is not satisfied in all situations of interest. In addition, although it is possible to glue to a Banach manifold a handle of infinite index, in view of the homotopic triviality of infinite-dimensional spheres this handle has no effect on the homotopy type. Therefore only critical points of finite index occur in the fundamental theorem of Morse theory 3. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) {{MR|1451874}} {{MR|1501555}} {{MR|1561686}} {{MR|1501489}} {{MR|1501428}} {{ZBL|0011.02802}} {{ZBL|60.0450.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) {{MR|0163331}} {{ZBL|0108.10401}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Milnor, "Lectures on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065010/m065010159.png" />-cobordism theorem" , Princeton Univ. Press (1965) {{MR|190942}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Seifert, W. Threlfall, "Variationsrechnung im Groszen (Morsesche Theorie)" , Teubner (1938)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) {{MR|0229177}} {{ZBL|0155.30701}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) {{MR|0169148}} {{ZBL|0132.16003}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M.M. Postnikov, "Introduction to Morse theory" , Moscow (1971) (In Russian) {{MR|0315739}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> M.M. Postnikov, "The variational theory of geodesics" , Saunders (1967) (Translated from Russian) {{MR|0210042}} {{ZBL|0167.50102}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J. Eells, "A setting for global analysis" ''Bull. Amer. Math. Soc.'' , '''72''' (1966) pp. 751–807 {{MR|0203742}} {{ZBL|0191.44101}} </TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> J.-P. Serre, "Homologie singulière des espaces fibrés I" ''C.R. Acad. Sci. Paris'' , '''231''' (1950) pp. 1408–1410 {{MR|0039253}} {{ZBL|0039.39702}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> J.-P. Serre, "Homologie singulière des espaces fibrés. Applications" ''Ann. of Math. (2)'' , '''54''' (1951) pp. 425–505 {{MR|0045386}} {{ZBL|0045.26003}} </TD></TR><TR><TD valign="top">[10c]</TD> <TD valign="top"> J.-P. Serre, "Homologie singulière des espaces fibrés II" ''C.R. Acad. Sci. Paris'' , '''232''' (1951) pp. 31–33 {{MR|0039254}} {{ZBL|0042.17401}} </TD></TR><TR><TD valign="top">[10d]</TD> <TD valign="top"> J.-P. Serre, "Homologie singulière des espaces fibrés III" ''C.R. Acad. Sci. Paris'' , '''232''' (1951) pp. 142–144 {{MR|0039255}} {{ZBL|0042.17402}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A useful survey of Morse theory is [[#References|[a1]]]; historical remarks can be found in [[#References|[a2]]] and [[#References|[a3]]], Sect. 1.7. | A useful survey of Morse theory is [[#References|[a1]]]; historical remarks can be found in [[#References|[a2]]] and [[#References|[a3]]], Sect. 1.7. | ||
| − | There is an analogue (generalization) of (finite-dimensional) smooth Morse theory for suitable spaces with singularities, called stratified Morse theory. Let | + | There is an analogue (generalization) of (finite-dimensional) smooth Morse theory for suitable spaces with singularities, called stratified Morse theory. Let $ X $ |
| + | be a compact Whitney-stratified space contained in a smooth manifold $ M $( | ||
| + | cf. (the editorial comments to) [[Stratification|Stratification]]). Let $ f $ | ||
| + | be the restriction to $ X $ | ||
| + | of a smooth real-valued function on $ M $. | ||
| + | A critical point of $ f $ | ||
| + | is any critical point of $ f $ | ||
| + | restricted to a stratum of $ X $. | ||
| + | In particular, all the zero-dimensional strata are critical points. The proper smooth function $ f $ | ||
| + | is called a Morse function on the stratified space $ X $ | ||
| + | if: | ||
| − | a) all critical values of | + | a) all critical values of $ f $ |
| + | are distinct; | ||
| − | b) at each critical point | + | b) at each critical point $ p $ |
| + | of $ f $, | ||
| + | the restriction of $ f $ | ||
| + | to the stratum containing $ p $ | ||
| + | has a non-degenerate critical point at $ p $; | ||
| − | c) the differential of | + | c) the differential of $ f $ |
| + | at a critical point $ p $ | ||
| + | does not annihilate any limit of tangent spaces to any stratum $ S $ | ||
| + | other than the stratum containing $ p $. | ||
| − | It follows that the set of critical points is discrete in | + | It follows that the set of critical points is discrete in $ X $ |
| + | and that the critical values are discrete in $ \mathbf R $. | ||
| + | If $ M = \mathbf R ^ {m} $, | ||
| + | the distance function on $ X $ | ||
| + | from a point $ q \in \mathbf R ^ {m} $ | ||
| + | is a Morse function for almost-all $ q $. | ||
| + | The Morse functions also form an open dense set in the space of all proper smooth functions with the appropriate topology. | ||
| − | For each | + | For each $ c \in \mathbf R $, |
| + | let $ X _ {c} = \{ {x \in X } : {f ( x) \leq c } \} $. | ||
| + | Then (for a Morse function $ f $ | ||
| + | on $ X $) | ||
| + | one has the following analogue of smooth finite-dimensional Morse theory. As $ c $ | ||
| + | varies in the open interval between two adjacent critical values, the topological type of $ X _ {c} $ | ||
| + | does not vary, and as $ c $ | ||
| + | crosses a critical value $ c _ {0} $( | ||
| + | from below), the topological type of $ X _ {c + \epsilon } $, | ||
| + | with $ \epsilon $ | ||
| + | sufficiently small, is obtained from that of $ X _ {c - \epsilon } $ | ||
| + | by glueing in a suitable (stratified) space $ A $ | ||
| + | along a subspace $ B $. | ||
| + | The major difference is that the pair $ ( A , B ) $ | ||
| + | can be far more complicated than the pair $ ( D ^ \lambda \times D ^ {n - \lambda } , \partial D ^ \lambda \times D ^ {n - \lambda } ) $, | ||
| + | where $ D ^ {i} $ | ||
| + | is the $ i $- | ||
| + | dimensional solid ball, of the smooth theory. Also, the pair $ ( A , B ) $ | ||
| + | is not determined by a single integer. [[Intersection homology|Intersection homology]] plays an analogous role vis à vis stratified Morse theory as ordinary homology does with respect to the smooth theory, in that if $ ( A , B ) $ | ||
| + | is the pair belonging to the critical point $ p \in S $, | ||
| + | then the intersection homology group $ \mathop{\rm IH} _ {i} ( A , B ) $ | ||
| + | vanishes for all $ i $ | ||
| + | except $ i = n - s + \lambda _ {p} $, | ||
| + | where $ s = \mathop{\rm dim} S $, | ||
| + | $ n = \mathop{\rm dim} X $ | ||
| + | and $ \lambda _ {p} $ | ||
| + | is the [[Morse index|Morse index]] of $ f $ | ||
| + | restricted to $ S $ | ||
| + | at $ p $. | ||
There are two other important generalizations of ordinary finite-dimensional Morse theory: | There are two other important generalizations of ordinary finite-dimensional Morse theory: | ||
===The non-isolated case.=== | ===The non-isolated case.=== | ||
| − | This applies to functions with non-degenerate critical manifolds. One assumes that | + | This applies to functions with non-degenerate critical manifolds. One assumes that $ f $ |
| + | restricted to the normal direction is non-degenerate. Cf. [[#References|[a5]]]. | ||
===The equivariant case.=== | ===The equivariant case.=== | ||
| Line 68: | Line 296: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Bott, "Lectures on Morse theory, old and new" ''Bull. Amer. Math. Soc.'' , '''7''' : 2 (1982) pp. 331–358 {{MR|0714336}} {{MR|0663786}} {{ZBL|0521.58019}} {{ZBL|0505.58001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Bott, "Marston Morse and his mathematical works" ''Bull. Amer. Math. Soc.'' , '''3''' : 3 (1980) pp. 907–950 {{MR|0585177}} {{ZBL|0469.01012}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Goreski, R. MacPherson, "Stratified Morse theory" , Springer (1988)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Atiyah, R. Bott, "The Yang–Mills equations over Riemann surfaces" ''Phil. Trans. R. Soc. London A'' , '''308''' (1982) pp. 523–615 {{MR|0702806}} {{ZBL|0509.14014}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R. Bott, "Non-degenerate critical manifolds" ''Ann. of Math. (2)'' , '''60''' (1954) pp. 248–261 {{MR|64399}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) {{MR|0478069}} {{ZBL|0397.58018}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Smale, "Morse theory and a non-linear generalization of the Dirichlet problem" ''Ann. of Math.'' , '''80''' (1964) pp. 382–346 {{MR|0165539}} {{ZBL|0131.32305}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) {{MR|0666697}} {{ZBL|0495.53036}} </TD></TR></table> |
Latest revision as of 08:01, 6 June 2020
The common name for three different theories based on ideas of M. Morse [1] and describing the relation between algebraic-topological properties of topological spaces and extremal properties of functions (functionals) on them. Morse theory is a branch of variational calculus in the large (calculus of variations in the large); however, the latter is broader: for example, it includes the theory of categories (cf. Category (in the sense of Lyusternik–Shnirel'man)).
1) Morse theory of critical points (cf. Critical point) of smooth functions $ f $ on a smooth manifold $ M $( briefly, Morse theory 1) is divided into two parts: local and global. The local part is related to the idea of a critical point of a smooth function, the Hessian of a function at its critical point, the Morse index of a critical point, etc. The basic result is the Morse lemma, which describes the structure of a smooth function in a neighbourhood of a non-degenerate critical point.
The study of smooth functions in neighbourhoods of degenerate points does not properly belong to Morse theory, it does rather belong to the separate theory of singularities of differentiable mappings.
The basic results in global Morse theory are as follows. Let $ f $ be a function on a smooth manifold $ M $. If the set $ f ^ { - 1 } ( a) $ does not contain a critical point of $ f $ and does not intersect the boundary of $ M $, then $ M ^ {a} = f ^ { - 1 } ( - \infty , a) $ is a smooth manifold with boundary $ f ^ { - 1 } ( a) $. If the set $ f ^ { - 1 } [ a , b ] $ is compact, does not intersect the boundary of $ M $ and does not contain a critical point of $ f $, then there is a smooth isotopy $ h _ {t} : M \rightarrow M $, $ 0 \leq t \leq 1 $( realized by shifting along the trajectories of the gradient of $ f $), such that $ h _ {0} = \mathop{\rm id} _ {M} $ and $ h _ {1} $ diffeomorphically maps $ M ^ {b} $ onto $ M ^ {a} $. In particular, $ M ^ {b} $ is diffeomorphic to $ M ^ {a} $ and the inclusion $ M ^ {a} \subset M ^ {b} $ is a homotopy equivalence.
If $ f ^ { - 1 } [ a , b ] $ is compact, does not intersect the boundary of $ M $ and contains precisely one critical point $ p \in f ^ { - 1 } ( a , b ) $ with Morse index $ \lambda $, then $ M ^ {b} $ is diffeomorphic to a manifold obtained from $ M ^ {a} $ by glueing a handle of index $ \lambda $( see Morse surgery). In particular, if $ p $ is the unique global minimum point of $ f $, then for small $ \epsilon > 0 $ the set $ M ^ { f ( p) + \epsilon } $ is diffeomorphic to the disc $ D ^ {n} $, where $ n = \mathop{\rm dim} M $. Hence it follows that if $ M $ is a closed smooth manifold having a function with precisely two critical points (both non-degenerate), then $ M $ is obtained by glueing two smooth discs along their common boundary and, therefore, it is homeomorphic (but in general not diffeomorphic) to the sphere $ S ^ {n} $.
Since glueing a handle of index $ \lambda $ is homotopically equivalent to glueing a cell of dimension $ \lambda $, the following fundamental theorem of Morse theory 1 follows immediately: Corresponding to each Morse function $ f $ on a smooth manifold $ M $( without boundary) is a CW-complex homotopically equivalent to $ M $; its cells are in bijective correspondence with the critical points of $ f $ and the dimension of a cell is equal to the index of the corresponding critical point. The Morse inequalities are an immediate consequence of this theorem. An analogous theorem is valid for a Morse function on a triple $ ( W ; V _ {0} , V _ {1} ) $.
2) Morse theory of geodesics on a Riemannian manifold (briefly, Morse theory 2) describes the homotopy type of the loop space $ \Omega M $ of a smooth manifold $ M $ with a Riemannian metric $ g _ {ij} $. Its aim is to transfer the results of Morse theory 1 to this space (more correctly, to a suitable model of it). The role of $ f $ is played here by an action functional $ E $( sometimes called energy functional, [5]), defined on the space $ \mathop{\rm PS} ( M) $ of piecewise-smooth paths $ \omega : t \rightarrow \omega ( t) $, $ 0 \leq t \leq 1 $, whose value on a path $ \omega \in \mathop{\rm PS} ( M) $ is defined, in local coordinates $ x ^ {1} \dots x ^ {n} $, by the formula
$$ E ( \omega ) = \ \int\limits _ { 0 } ^ { 1 } g _ {ij} d x ^ {i} d x ^ {j} . $$
In the initial construction of Morse theory the length functional
$$ L ( \omega ) = \ \int\limits _ { 0 } ^ { 1 } \sqrt {g _ {ij} d x ^ {i} d x ^ {j} } $$
was considered, but for many technical reasons $ E $ turned out to be preferable. At the same time the extremals of $ E $( that is, paths $ \omega \in \mathop{\rm PS} ( M) $ for which the linear functional $ E _ {*} $ defined by the variation $ \delta E $ of $ E $ is zero on $ T _ \omega $) coincide with the geodesics of the metric $ g _ {ij} $( the extremals of the functional $ L $) in their natural parametrization.
Let $ p $ and $ q $ be two (not necessarily distinct) points of $ M $, and let $ \Omega ^ { \mathop{\rm PS} } ( M ; p , q ) \subset \mathop{\rm PS} ( M) $ be the space of piecewise-smooth paths joining $ p $ to $ q $. For each $ l \in \mathbf R $, put
$$ \Omega _ {l} = \ \Omega _ {l} ^ { \mathop{\rm PS} } ( M ; p , q ) = E ^ {-} 1 [ 0 , l ] \cap \Omega ^ { \mathop{\rm PS} } ( M ; p , q ) . $$
If $ M $ is complete, then $ \Omega _ {l} ^ {0} = E ^ {-} 1 [ 0 , l ) \cap \Omega _ {l} $( the interior of $ \Omega _ {l} $) is a deformation retract of a smooth manifold $ B $ whose points are "polygonal geodesics" with a fixed number of links, joining $ p $ to $ q $( so that, in particular, $ B $ contains all geodesics from $ \Omega _ {l} ^ {0} $). Here $ E ^ \prime = E \mid _ {B} : B \rightarrow \mathbf R $ is a smooth function; for any $ a < l $ the set $ B ^ {a} = ( E ^ \prime ) ^ {-} 1 [ 0 , a ] $ is compact and is a deformation retract of $ \Omega _ {a} $; the critical points of $ E ^ \prime $ coincide with the extremals of the functional $ E : \Omega _ {l} ^ {0} \rightarrow \mathbf R $ and are geodesics of length $ < \sqrt l $ joining $ p $ and $ q $; the Morse indices of the critical points of $ E ^ \prime $ are equal to the Morse indices of the corresponding geodesics; the null space $ N _ \gamma $ of $ E _ {**} $ on a geodesic $ \gamma \in \Omega _ {l} ^ {0} $ is finite dimensional and isomorphic to the null space of the Hessian of $ E ^ \prime $ at the corresponding critical point; in particular, if $ p $ and $ q $ are not conjugate on any geodesic $ \gamma $ joining them, then $ E ^ \prime $ is a Morse function. Applying Morse theory 1, passing to the limit as $ l \rightarrow \infty $ and noting that $ \Omega ^ { \mathop{\rm PS} } ( M ; p , q ) $ is homotopically equivalent to the space $ \Omega ( M ; p , q ) $ of all continuous paths joining $ p $ to $ q $, one obtains the following fundamental theorem of Morse theory 2: Let $ M $ be a complete Riemannian manifold and let $ p $ and $ q $ be two points not conjugate on any geodesic joining them. The space $ \Omega ( M ; p , q ) $ of all paths joining $ p $ and $ q $ is homotopically equivalent to a CW-complex all cells of dimension $ \lambda $ of which are in bijective correspondence with the geodesics of index $ \lambda $ joining $ p $ to $ q $. Since the homotopy type of $ \Omega ( M ; p , q ) $ does not depend on the choice of $ p $ and $ q $, this theorem gives, in particular, a description of the homotopy type of the loop space $ \Omega M $.
It is known
that for a non-contractible manifold $ M $ the space $ \Omega M $ has non-trivial homology groups in arbitrarily high dimension. By the fundamental theorem of Morse theory 2 it follows that non-conjugate points in a complete Riemannian non-contractible manifold are joined by infinitely many geodesics (by the example of the sphere it is clear, in general, that these geodesics may be segments of one periodic geodesic).
In the description of the homotopy type given by the fundamental theorem, Jacobi fields (cf. Jacobi equation and Jacobi vector field) (implicitly) appear, therefore Morse theory establishes a connection between the curvature of a manifold and its topology. For example, if $ M $ is a complete simply-connected Riemannian manifold of non-positive curvature in all two-dimensional directions, then any Jacobi field vanishing at two points of a geodesic is identically zero. Therefore the loop space $ \Omega M $ of such a manifold has the type of a zero-dimensional CW-complex, and consequently (in view of the simple connectedness of $ M $) is contractible. Therefore $ M $ is contractible, that is, is homotopically equivalent to $ \mathbf R ^ {n} $. A more precise use of Morse theory shows that $ M $ is even diffeomorphic to $ \mathbf R ^ {n} $( see [3], [5]).
The application of Morse theory to the topology of Lie groups has turned out to be very effective [2]. For example, for any simply-connected Lie group $ G $ the space $ \Omega G $ has the homotopy type of a CW-complex with only odd-dimensional cells. The apotheosis here is the Bott periodicity theorem, which plays a fundamental role in $ K $- theory and, consequently, in the whole of differential topology. Let $ U $ be the limit of the sequence of nested unitary groups $ \dots \subset U _ {n} \subset U _ {n+} 1 \subset \dots $ and let $ O $ be the limit of the sequence of nested orthogonal groups $ \dots \subset O _ {n} \subset O _ {n+} 1 \subset \dots $. Bott's periodicity theorem asserts that there are homotopy equivalences $ \Omega ^ {2} U \sim U $, $ \Omega ^ {8} O \sim O $, where $ \Omega ^ {n} $ is the $ n $- th iterate of the functor of passing to the loop space. This theorem allows one to calculate the homotopy groups $ \pi _ {i} U $ and $ \pi _ {i} O $ and, consequently, the homotopy groups $ \pi _ {i} U _ {n} $ and $ \pi _ {j} O _ {n} $ for $ i < 2 n $, $ j < n $.
More theory 2 generalizes also to the case when instead of points $ p , q $ smooth submanifolds $ V _ {0} , V _ {1} $ of $ M $ are considered. The action functional is studied on the space $ \Omega ^ { \mathop{\rm PS} } ( M ; V _ {0} , V _ {1} ) $ of all piecewise-smooth paths $ \omega : t \rightarrow \omega ( t) $, $ 0 \leq t \leq 1 $, $ \omega ( i) \in V _ {i} $, $ i = 0 , 1 $, that are transversal at the end-points to $ V _ {0} $ and $ V _ {1} $, and a relation between the extremals of this functional and the homotopy type of $ \Omega ( M ; V _ {0} , V _ {1} ) $ has been established. The corresponding fundamental theorem is analogous to the above-mentioned fundamental theorem of Morse theory 2; the difficulty is in the geometric interpretation of the Morse index of a geodesic.
3) The natural development of Morse theory 2 is Morse theory for critical points of smooth functions on Banach (infinite-dimensional) manifolds — Morse theory 3, which is no longer an analogue, but a direct generalization of Morse theory 1. At present (1989) Morse theory 3 is at an initial stage and has been constructed only in a very preliminary context under very strong (and clearly not necessary) conditions on the model Banach space (on separable- and Hilbert-type spaces), when no specifically functional-analytic difficulties arise [9], although there have been attempts at a construction of Morse theory 3 in fairly general situations. Therefore, in its modern form, Morse theory 3 is an almost verbatim re-iteration of Morse theory 1. The only difference worth mentioning is that in Morse theory 3 the compactness of $ f ^ { - 1 } [ a , b ] $ is replaced by condition $ C $ of Palais–Smale (see Morse function), which, besides, is not satisfied in all situations of interest. In addition, although it is possible to glue to a Banach manifold a handle of infinite index, in view of the homotopic triviality of infinite-dimensional spheres this handle has no effect on the homotopy type. Therefore only critical points of finite index occur in the fundamental theorem of Morse theory 3.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) MR1451874 MR1501555 MR1561686 MR1501489 MR1501428 Zbl 0011.02802 Zbl 60.0450.01 |
| [2] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) MR0163331 Zbl 0108.10401 |
| [3] | J. Milnor, "Lectures on the 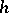 -cobordism theorem" , Princeton Univ. Press (1965) MR190942 -cobordism theorem" , Princeton Univ. Press (1965) MR190942 |
| [4] | H. Seifert, W. Threlfall, "Variationsrechnung im Groszen (Morsesche Theorie)" , Teubner (1938) |
| [5] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) MR0229177 Zbl 0155.30701 |
| [6] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) MR0169148 Zbl 0132.16003 |
| [7] | M.M. Postnikov, "Introduction to Morse theory" , Moscow (1971) (In Russian) MR0315739 |
| [8] | M.M. Postnikov, "The variational theory of geodesics" , Saunders (1967) (Translated from Russian) MR0210042 Zbl 0167.50102 |
| [9] | J. Eells, "A setting for global analysis" Bull. Amer. Math. Soc. , 72 (1966) pp. 751–807 MR0203742 Zbl 0191.44101 |
| [10a] | J.-P. Serre, "Homologie singulière des espaces fibrés I" C.R. Acad. Sci. Paris , 231 (1950) pp. 1408–1410 MR0039253 Zbl 0039.39702 |
| [10b] | J.-P. Serre, "Homologie singulière des espaces fibrés. Applications" Ann. of Math. (2) , 54 (1951) pp. 425–505 MR0045386 Zbl 0045.26003 |
| [10c] | J.-P. Serre, "Homologie singulière des espaces fibrés II" C.R. Acad. Sci. Paris , 232 (1951) pp. 31–33 MR0039254 Zbl 0042.17401 |
| [10d] | J.-P. Serre, "Homologie singulière des espaces fibrés III" C.R. Acad. Sci. Paris , 232 (1951) pp. 142–144 MR0039255 Zbl 0042.17402 |
Comments
A useful survey of Morse theory is [a1]; historical remarks can be found in [a2] and [a3], Sect. 1.7.
There is an analogue (generalization) of (finite-dimensional) smooth Morse theory for suitable spaces with singularities, called stratified Morse theory. Let $ X $ be a compact Whitney-stratified space contained in a smooth manifold $ M $( cf. (the editorial comments to) Stratification). Let $ f $ be the restriction to $ X $ of a smooth real-valued function on $ M $. A critical point of $ f $ is any critical point of $ f $ restricted to a stratum of $ X $. In particular, all the zero-dimensional strata are critical points. The proper smooth function $ f $ is called a Morse function on the stratified space $ X $ if:
a) all critical values of $ f $ are distinct;
b) at each critical point $ p $ of $ f $, the restriction of $ f $ to the stratum containing $ p $ has a non-degenerate critical point at $ p $;
c) the differential of $ f $ at a critical point $ p $ does not annihilate any limit of tangent spaces to any stratum $ S $ other than the stratum containing $ p $.
It follows that the set of critical points is discrete in $ X $ and that the critical values are discrete in $ \mathbf R $. If $ M = \mathbf R ^ {m} $, the distance function on $ X $ from a point $ q \in \mathbf R ^ {m} $ is a Morse function for almost-all $ q $. The Morse functions also form an open dense set in the space of all proper smooth functions with the appropriate topology.
For each $ c \in \mathbf R $, let $ X _ {c} = \{ {x \in X } : {f ( x) \leq c } \} $. Then (for a Morse function $ f $ on $ X $) one has the following analogue of smooth finite-dimensional Morse theory. As $ c $ varies in the open interval between two adjacent critical values, the topological type of $ X _ {c} $ does not vary, and as $ c $ crosses a critical value $ c _ {0} $( from below), the topological type of $ X _ {c + \epsilon } $, with $ \epsilon $ sufficiently small, is obtained from that of $ X _ {c - \epsilon } $ by glueing in a suitable (stratified) space $ A $ along a subspace $ B $. The major difference is that the pair $ ( A , B ) $ can be far more complicated than the pair $ ( D ^ \lambda \times D ^ {n - \lambda } , \partial D ^ \lambda \times D ^ {n - \lambda } ) $, where $ D ^ {i} $ is the $ i $- dimensional solid ball, of the smooth theory. Also, the pair $ ( A , B ) $ is not determined by a single integer. Intersection homology plays an analogous role vis à vis stratified Morse theory as ordinary homology does with respect to the smooth theory, in that if $ ( A , B ) $ is the pair belonging to the critical point $ p \in S $, then the intersection homology group $ \mathop{\rm IH} _ {i} ( A , B ) $ vanishes for all $ i $ except $ i = n - s + \lambda _ {p} $, where $ s = \mathop{\rm dim} S $, $ n = \mathop{\rm dim} X $ and $ \lambda _ {p} $ is the Morse index of $ f $ restricted to $ S $ at $ p $.
There are two other important generalizations of ordinary finite-dimensional Morse theory:
The non-isolated case.
This applies to functions with non-degenerate critical manifolds. One assumes that $ f $ restricted to the normal direction is non-degenerate. Cf. [a5].
The equivariant case.
This applies to functions which are equivariant under the action of a Lie group. Cf. [a1]. There are applications e.g. to Yang–Mills theory (cf. Yang–Mills field) in 2 dimensions. Cf. [a4].
References
| [a1] | R. Bott, "Lectures on Morse theory, old and new" Bull. Amer. Math. Soc. , 7 : 2 (1982) pp. 331–358 MR0714336 MR0663786 Zbl 0521.58019 Zbl 0505.58001 |
| [a2] | R. Bott, "Marston Morse and his mathematical works" Bull. Amer. Math. Soc. , 3 : 3 (1980) pp. 907–950 MR0585177 Zbl 0469.01012 |
| [a3] | M. Goreski, R. MacPherson, "Stratified Morse theory" , Springer (1988) |
| [a4] | M. Atiyah, R. Bott, "The Yang–Mills equations over Riemann surfaces" Phil. Trans. R. Soc. London A , 308 (1982) pp. 523–615 MR0702806 Zbl 0509.14014 |
| [a5] | R. Bott, "Non-degenerate critical manifolds" Ann. of Math. (2) , 60 (1954) pp. 248–261 MR64399 |
| [a6] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) MR0478069 Zbl 0397.58018 |
| [a7] | S. Smale, "Morse theory and a non-linear generalization of the Dirichlet problem" Ann. of Math. , 80 (1964) pp. 382–346 MR0165539 Zbl 0131.32305 |
| [a8] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) MR0666697 Zbl 0495.53036 |
Morse theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_theory&oldid=15676