Morley rank
An important notion and tool in model theory, a branch of mathematical logic. The Morley rank is an ordinal-valued dimension associated to first-order formulas with parameters from a model 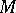 of a complete first-order theory
of a complete first-order theory 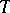 . It is defined inductively by:
. It is defined inductively by: 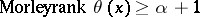 if there is an elementary extension
if there is an elementary extension 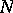 of
of 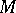 and infinitely many formulas
and infinitely many formulas 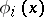 (
(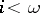 ) with parameters from
) with parameters from 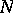 such that the
such that the 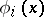 are pairwise inconsistent,
are pairwise inconsistent, 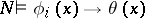 for all
for all 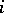 and
and 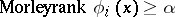 for all
for all 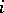 . For
. For 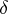 a limit ordinal (cf. also Ordinal number),
a limit ordinal (cf. also Ordinal number), 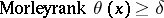 if
if 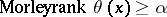 for all
for all 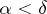 . The Morley rank of
. The Morley rank of 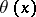 is said to be equal to
is said to be equal to  if it is greater than or equal to
if it is greater than or equal to  but not greater than or equal to
but not greater than or equal to 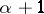 . The Morley rank of
. The Morley rank of 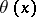 is said to be
is said to be 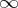 (or undefined) if it is not equal to any ordinal.
(or undefined) if it is not equal to any ordinal.
The Morley rank was introduced by M. Morley [a2] in his study of countable theories 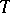 such that for some uncountable cardinal number
such that for some uncountable cardinal number 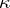 ,
, 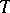 has a unique model of cardinality
has a unique model of cardinality 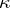 . Morley showed that a theory
. Morley showed that a theory 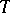 satisfying the latter condition has a unique model of cardinality
satisfying the latter condition has a unique model of cardinality 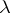 for any uncountable cardinal
for any uncountable cardinal 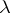 . An important part of his work was to show that every formula has ordinal-valued Morley rank. Subsequently, J.T. Baldwin [a1] showed that under Morley's hypothesis, every formula has finite Morley rank.
. An important part of his work was to show that every formula has ordinal-valued Morley rank. Subsequently, J.T. Baldwin [a1] showed that under Morley's hypothesis, every formula has finite Morley rank.
A classical example of Morley rank occurs in the (complete) theory 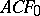 of algebraically closed fields of characteristic
of algebraically closed fields of characteristic  . The field
. The field 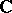 of complex numbers is a model, and for a formula
of complex numbers is a model, and for a formula 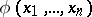 with parameters in
with parameters in 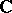 defining a non-singular algebraic variety
defining a non-singular algebraic variety 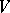 , the Morley rank of
, the Morley rank of 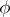 is precisely the dimension of
is precisely the dimension of 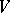 as a complex manifold.
as a complex manifold.
Following the example of Morley rank, S. Shelah [a3] defined a host of rank-functions associated to formulas in first-order theories, which play an important role in classification theory.
See also Group of finite Morley rank.
References
| [a1] | J.T. Baldwin, "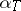 is finite for is finite for 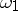 -categorical -categorical 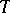 " Trans. Amer. Math. Soc. , 181 (1973) pp. 37–51 " Trans. Amer. Math. Soc. , 181 (1973) pp. 37–51 |
| [a2] | M.D. Morley, "Categoricity in power" Trans. Amer. Math. Soc. , 114 (1965) pp. 514–538 |
| [a3] | S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1990) (Edition: Revised) |
Morley rank. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morley_rank&oldid=14510