Morita equivalence
An equivalence relation on the class of all rings (cf. Ring) defined as follows: Two rings  and
and  are called Morita equivalent if the categories of left (right)
are called Morita equivalent if the categories of left (right)  - and
- and  -modules are equivalent. The most important examples of Morita-equivalent rings are: a ring
-modules are equivalent. The most important examples of Morita-equivalent rings are: a ring  and the ring of all
and the ring of all  -matrices over it. In order that there is Morita equivalence between two rings
-matrices over it. In order that there is Morita equivalence between two rings  and
and  it is necessary and sufficient that in the category of left
it is necessary and sufficient that in the category of left  -modules there is a finitely-generated projective generator
-modules there is a finitely-generated projective generator 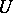 such that its ring of endomorphisms is isomorphic to
such that its ring of endomorphisms is isomorphic to 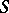 . The left
. The left 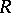 -module
-module  is put in correspondence with the left
is put in correspondence with the left 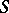 -module
-module 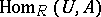 . Among the properties preserved by transition to a Morita-equivalent ring are the properties of being: Artinian, Noetherian, primary, simple, classically semi-simple, regular, self-injective, hereditary, and primitive.
. Among the properties preserved by transition to a Morita-equivalent ring are the properties of being: Artinian, Noetherian, primary, simple, classically semi-simple, regular, self-injective, hereditary, and primitive.
Alongside with Morita equivalence one considers Morita duality, relating some subcategories of the categories of left 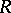 -modules and right
-modules and right 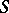 -modules (mostly the subcategories of finitely-generated modules). However, the very existence of such a duality places definite restrictions on the rings
-modules (mostly the subcategories of finitely-generated modules). However, the very existence of such a duality places definite restrictions on the rings  and
and  . In particular, for
. In particular, for 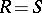 this implies that
this implies that 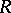 is a quasi-Frobenius ring.
is a quasi-Frobenius ring.
The general concept of Morita equivalence was developed by K. Morita [1].
References
| [1] | K. Morita, Sci. Reports Tokyo Kyoiku Dajkagu A , 6 (1958) pp. 83–142 |
| [2] | H. Bass, "Algebraic 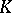 -theory" , Benjamin (1968) -theory" , Benjamin (1968) |
| [3] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1981–1976) |
| [4] | P. Cohn, "Morita equivalence and duality" , London (1976) |
Comments
For generating objects of categories see also Generator of a category.
Let 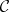 and
and 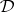 be categories. A duality is a pair of contravariant functors
be categories. A duality is a pair of contravariant functors 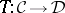 and
and  such that
such that 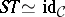 ,
, 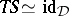 , where
, where 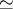 denotes natural equivalence (functorial isomorphism) and
denotes natural equivalence (functorial isomorphism) and  is the identity functor on
is the identity functor on 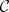 .
.
Let 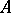 and
and 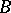 be rings and let
be rings and let 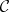 and
and 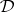 be full subcategories of the categories of right
be full subcategories of the categories of right 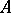 -modules
-modules 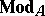 and left
and left 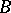 -modules
-modules 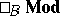 , respectively (cf. Module). Let
, respectively (cf. Module). Let 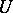 be a
be a 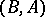 bimodule. A duality
bimodule. A duality 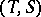 between
between 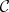 and
and 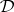 is called a
is called a 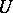 -duality or Morita duality if
-duality or Morita duality if 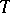 and
and  are, respectively, naturally equivalent to
are, respectively, naturally equivalent to 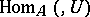 and
and 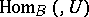 . A theorem of Morita says that if
. A theorem of Morita says that if 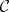 and
and  are Abelian full subcategories with
are Abelian full subcategories with 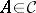 and
and  , then any duality
, then any duality 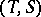 between
between  and
and  is a
is a  -duality with
-duality with  .
.
Morita equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morita_equivalence&oldid=17144