Mori theory of extremal rays

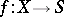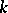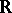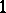Let be a projective morphism of algebraic varieties over a field of characteristic (cf. also Algebraic variety). A relative --cycle is a formal linear combination 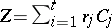of a finite number of curves 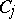(reduced irreducible -dimensional closed subschemes) on with real number coefficients 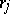such that 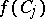are points on 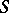. (If 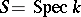, then the word "relative" is dropped.) Two relative 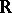--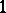cycles 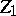and 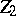are said to be numerically equivalent if their intersection numbers are equal, 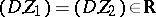for any Cartier divisor 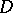on 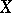(cf. also Divisor; Intersection index (in algebraic geometry)). The set 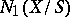of all the equivalence classes of relative --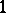cycles with respect to the numerical equivalence becomes a finite-dimensional real vector space. The closed cone of curves (the Kleiman–Mori cone) 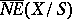is defined to be the closed convex cone in 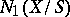generated by the classes of curves on 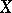which are mapped to points on 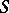by 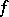. A half-line 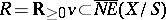is called an extremal ray if the inequality 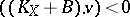holds and if the equality 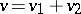for 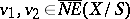implies .

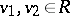Cone theorem.

Let 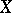be a normal algebraic variety and 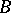an effective 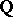-divisor such that the pair 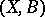is weakly log terminal (cf. Kawamata rationality theorem). Let 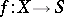be a projective morphism to another algebraic variety. Then there exist at most countably many extremal rays 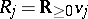(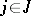) satisfying the following conditions:

For any 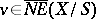, there exist an element 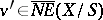and numbers 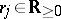, which are zero except for finitely many 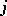, such that 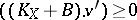and .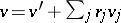

(discreteness) For any closed convex cone in 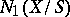such that 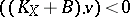for any 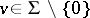, there exist only finitely many 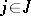such that .

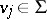Contraction theorem.

Let 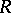be an extremal ray as above. Then there exists a morphism 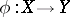, called a contraction morphism, to a normal algebraic variety 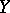with a morphism 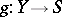which is characterized by the following properties:

;

;

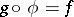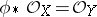any curve 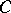which is mapped to a point by 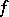is mapped to a point by 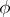if and only if its numerical class belongs to .

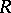Two methods of proofs for the cone theorem are known. The first one [a6] uses a deformation theory of morphisms over a field of positive characteristic and applies only in the case where 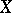is smooth. It is important to note that this is the only known method in mathematics to prove the existence of rational curves (as of 2000). The second approach [a2] uses a vanishing theorem of cohomology groups (cf. Kawamata–Viehweg vanishing theorem) which is true only in characteristic . This method of proof, which is obtained via a rationality theorem (cf. Kawamata rationality theorem), applies also to singular varieties and easily extends to the logarithmic version as explained above. The contraction theorem has been proved only by a characteristic- method (cf. [a1]).

In the following it is also assumed that the variety 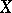is 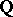-factorial, that is, for any prime divisor 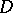on 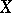there exists a positive integer 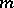, depending on 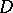, such that 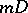is a Cartier divisor. Then the contraction morphism 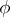is of one of the following types:

(Fano–Mori fibre space) .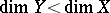

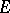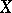(divisorial contraction) There exists a prime divisor of such that 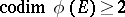and 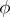induces an isomorphism .

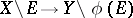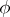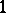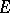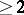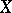(small contraction) is an isomorphism in codimension , in the sense that there exists a closed subset of codimension of such that 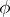induces an isomorphism .

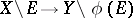Flip conjectures.

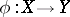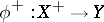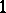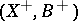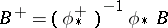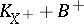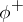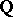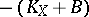The first flip conjecture is as follows: Let be a small contraction. Then there exists a birational morphism from a -factorial normal algebraic variety which is again an isomorphism in codimension and is such that the pair with is weakly log terminal and is a -ample -divisor (cf. also Divisor). The diagram is called a flip (or log flip). Note that is 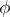-ample.

The second flip conjecture states that there does not exist an infinite sequence of consecutive flips.

There is no small contraction if 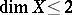. The flip conjectures have been proved for 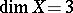(see [a3], [a4] for the first flip conjecture, and [a5], [a7] for the second). The proofs depend on the classification of singularities and it is hard to extend them to a higher-dimensional case.

Minimal model program (MMP).

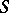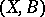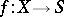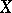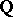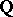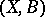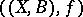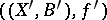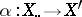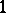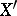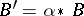Fix a base variety and consider a category whose objects are a pair and a projective morphism such that is a -factorial normal algebraic variety and is a -divisor such that is weakly log terminal. A morphism from to in this category is a birational mapping which is surjective in codimension , in the sense that any prime divisor on is the image of a prime divisor on , and such that and 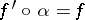. The minimal model program is a program which works under the assumption that the flip conjectures hold. It starts from an arbitrary object 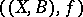and constructs a morphism to another object 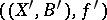such that one of the following holds:

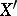has a Fano–Mori fibre space structure 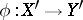over .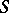

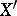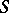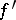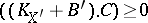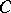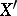is minimal over in the sense that is -nef, i.e., an inequality holds for any curve on such that 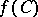is a point on . Construct objects 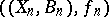inductively as follows. Set 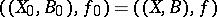. Suppose that 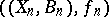has already been constructed. If 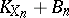is 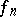-nef, then a minimal model is obtained. If not, then, by the cone theorem, there exists an extremal ray and one obtains a contraction morphism 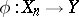by the contraction theorem. If 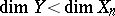, then a Fano–Mori fibre space is obtained. If 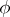is a divisorial contraction, then one sets 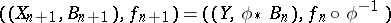. If 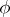is a small contraction and if the first flip conjecture is true, then take the flip 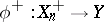and set 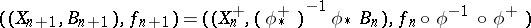. If the second flip conjecture is true, then this process stops after a finite number of steps.

A normal algebraic variety 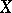is said to be terminal, or it is said that 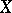has only terminal singularities, if the following conditions are satisfied:

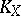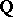1) The canonical divisor is a -Cartier divisor.

2) There exists a projective birational morphism 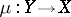from a smooth variety with a normal crossing divisor 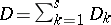such that one can write 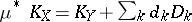with 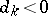for all .

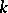As a special case of the minimal model program, if one assumes that 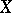has only terminal singularities and 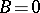, then any subsequent pair satisfies the same condition that has only terminal singularities and 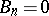. This is the "non-log" version.

It is expected that the minimal model program works also over a field of arbitrary characteristic, although the cone and contraction theorems are conjectural in general.

References

[a1]	Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" Adv. Stud. Pure Math. , 10 (1987) pp. 283–360
[a2]	Y. Kawamata, "The cone of curves of algebraic varieties" Ann. of Math. , 119 (1984) pp. 603–633
[a3]	S. Mori, "Flip theorem and the existence of minimal models for 3-folds" J. Amer. Math. Soc. , 1 (1988) pp. 117–253
[a4]	V. Shokurov, "3-fold log flips" Izv. Russian Akad. Nauk. , 56 (1992) pp. 105–203
[a5]	V. Shokurov, "The nonvanishing theorem" Izv. Akad. Nauk. SSSR , 49 (1985) pp. 635–651
[a6]	S. Mori, "Threefolds whose canonical bundles are not numerically effective" Ann. of Math. , 116 (1982) pp. 133–176
[a7]	Y. Kawamata, "Termination of log-flips for algebraic 3-folds" Internat. J. Math. , 3 (1992) pp. 653–659