Moore space
A topological space 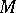 with a unique non-trivial reduced homology group:
with a unique non-trivial reduced homology group:
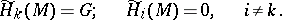 |
If  is the Eilenberg–MacLane space of the group of integers
is the Eilenberg–MacLane space of the group of integers  and
and 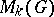 is the Moore space with
is the Moore space with 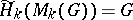 , then
, then
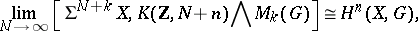 |
that is, 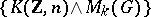 is the spectrum of the cohomology theory
is the spectrum of the cohomology theory  . This allows one to extend the idea of cohomology with arbitrary coefficients to a generalized cohomology theory. For any spectrum
. This allows one to extend the idea of cohomology with arbitrary coefficients to a generalized cohomology theory. For any spectrum 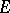 , the spectrum
, the spectrum 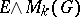 defines a cohomology theory
defines a cohomology theory 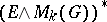 , called the
, called the 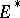 -cohomology theory with coefficient group
-cohomology theory with coefficient group 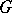 . For the definition of generalized homology theories with coefficients in a group
. For the definition of generalized homology theories with coefficients in a group  , the so-called co-Moore space
, the so-called co-Moore space 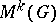 is used, which is characterized by
is used, which is characterized by
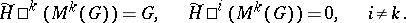 |
For example, the group 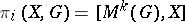 is called the homotopy group of the space
is called the homotopy group of the space 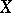 with coefficients in
with coefficients in  . However, the space
. However, the space 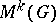 does not exist for all pairs
does not exist for all pairs 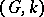 . If
. If 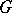 is a finitely-generated group, then
is a finitely-generated group, then 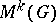 does exist.
does exist.
References
| [1] | J.C. Moore, "On homotopy groups of spaces with a single non-vanishing homotopy group" Ann. of Math. , 59 : 3 (1954) pp. 549–557 |
Comments
For a construction of a Moore space as a CW-complex with one zero cell and further only cells in dimensions  and
and 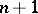 , cf. [a1]. The Eilenberg–MacLane space
, cf. [a1]. The Eilenberg–MacLane space 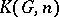 can be obtained from the Moore space
can be obtained from the Moore space 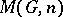 by killing the higher homotopy groups.
by killing the higher homotopy groups.
In general topology, a Moore space is a regular space with a development. (A development is a sequence 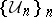 of open coverings such that for every
of open coverings such that for every  and every open set
and every open set 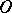 containing
containing  there is an
there is an  such that
such that
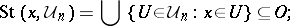 |
in other words, 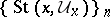 is a neighbourhood base at
is a neighbourhood base at  .)
.)
The idea of a development can be found in [a4] (Axiom 1). Moore spaces are generalizations of metric spaces and one can show that collectionwise normal Moore spaces are metrizable [a2]. The question whether every normal Moore space is metrizable generated lots of research; its solution is described in [a3].
References
| [a1] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. §17 |
| [a2] | R.H. Bing, "Metrization of topological spaces" Canad. J. Math. , 3 (1951) pp. 175–186 |
| [a3] | W.G. Fleissner, "The normal Moore space conjecture and large cardinals" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) pp. 733–760 |
| [a4] | R.L. Moore, "Foundations of point set theory" , Amer. Math. Soc. (1962) |
Moore space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moore_space&oldid=18047