Difference between revisions of "Moonshine conjectures"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 90 formulas, 88 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | In 1978, J. McKay observed that $196884 = 196883 + 1$. The number on the left is the first non-trivial coefficient of the $j$-function, and the numbers on the right are the dimensions of the smallest irreducible representations of the Fischer–Griess Monster $\bf M$ [[#References|[a10]]] (cf. also [[Sporadic simple group|Sporadic simple group]]). On the one side stands a [[Modular function|modular function]]; on the other, a finite [[Sporadic simple group|sporadic simple group]]. Moonshine is the explanation and generalization of this unlikely connection. | ||
| − | + | Monstrous moonshine [[#References|[a6]]] conjectured that there is an infinite-dimensional graded [[Vector space|vector space]] $V = V _ { - 1 } \oplus V _ { 1 } \oplus V _ { 2 } \oplus \ldots$, with the following properties. Each $V _ { k }$ carries a finite-dimensional representation of $\bf M$; write $\chi _ { k }$ for its character. For each $g \in \mathbf{M}$, define the [[Thompson–McKay series|Thompson–McKay series]] $T _ { g } ( z ) = \sum _ { k = - 1 } ^ { \infty } \chi _ { k } ( g ) q ^ { k }$, where $q = \operatorname { exp } ( 2 \pi i z )$. Then $T_g$ is a generator ( "Hauptmodul" ) of the field of modular functions for some genus-$0$ [[Group|group]] $G _ { g } \leq \operatorname {SL} _ { 2 } ( \mathbf{R} )$. The group $G _ { g }$ contains $\Gamma _ { 0 } ( N )$ as a [[Normal subgroup|normal subgroup]], where $N$ divides $o ( g ) \operatorname { gcd } ( 24 , o ( g ) )$ ($o ( g )$ is the order of $g$). | |
| − | + | There are $171$ distinct Thompson series ($\bf M$ has only $194$ conjugacy classes). For example, $G _ { e } = \operatorname{SL} _ { 2 } ( \mathbf{Z} )$ and $T _ { e } = j - 744$, where $e \in \mathbf{M}$ is the identity. $\bf M$ has two order-$2$ conjugacy classes, corresponding to the modular groups $\Gamma _ { 0 } ( 2 )$ and | |
| − | + | \begin{equation*} \Gamma _ { 0 } ( 2 ) ^ { + } : = \left( \Gamma _ { 0 } ( 2 ) , \left( \begin{array} { c c } { 0 } & { - 1 } \\ { 2 } & { 0 } \end{array} \right) \right). \end{equation*} | |
| − | + | Let $\rho _ { d }$ denote the $d$-dimensional irreducible representation of $\bf M$; then $V _ { - 1 } = \rho _ { 1 }$, $V _ { 1 } = \rho _ { 1 } \oplus \rho _ { 196883}$, and $V _ { 2 } = \rho _ { 1 } \oplus \rho _ { 196883 } \oplus \rho _ { 21296876 }$. | |
| − | + | Central to these conjectures is the moonshine module $V ^ { \natural }$, constructed in [[#References|[a9]]]. It is an important example of a [[Vertex operator algebra|vertex operator algebra]] (VOA) [[#References|[a2]]], [[#References|[a9]]], and as such possesses infinitely many heavily constrained bilinear products. One of these products makes $V _ { 1 }$ into the Griess algebra [[#References|[a10]]] extended by an identity element. The automorphism group of $V ^ { \natural }$ is $\bf M$. | |
| − | + | The monstrous moonshine conjectures, and, in particular, the identification of $V$ with $V ^ { \natural }$, were proved in [[#References|[a4]]], which also defined vertex operator algebras and a generalization of Kac–Moody algebras called Borcherds or generalized Kac–Moody algebras [[#References|[a3]]] (cf. also [[Kac–Moody algebra|Kac–Moody algebra]]; [[Borcherds Lie algebra|Borcherds Lie algebra]]). | |
| − | + | The series $T_g$ were generalized by S.P. Norton to commuting pairs $( g , h ) \in \bf M \times M$ [[#References|[a12]]]. In particular, to each such pair there is a [[Modular function|modular function]] $Z ( g,h ; z )$, invariant under a genus-$0$ group, such that | |
| − | + | \begin{equation*} Z ( g ^ { a } h ^ { c } , g ^ { b } h ^ { d } ; z ) = \alpha Z \left( g ,h ; \frac { a z + b } { c z + d } \right) \end{equation*} | |
| − | + | for some root of unity $\alpha$, for any | |
| − | + | \begin{equation*} \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} _ { 2 } ( {\bf Z} ). \end{equation*} | |
| − | + | This action of $\operatorname{SL} _ { 2 } ( \mathbf{Z} )$ is related to its natural action on the fundamental group $\mathbf{Z} ^ { 2 }$ of the torus. The coefficients of the $q$-expansion of $Z ( g,h ; z )$ are characters of the centralizer $C _ { \mathbf{M} } ( g )$ evaluated at $h$. Simultaneous conjugation of $g$, $h$ leaves $Z$ unchanged: $Z ( a g a ^ { - 1 } , a h a ^ { - 1 } ; z ) = Z ( g , h ; z )$. The [[Thompson–McKay series|Thompson–McKay series]] are recovered by the specialization $g = e$: $Z ( e , h ; z ) = T _ { h } ( z )$. Only special cases of these generalized moonshine conjectures have been proven. | |
| − | + | There are several other conjectures. For example, the series $T _ { g ^ { i } }$ were conjecturally related by the replication formulas [[#References|[a6]]], [[#References|[a1]]]: | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130220/m13022064.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a1)</td></tr></table> |
| − | + | where $Q _ { n }$ is the unique polynomial for which $Q _ { n } ( T _ { g } ( z ) ) - q ^ { - n }$ is a power series with only strictly positive powers of $q$. The resemblance of (a1) with Hecke operators is not accidental. These formulas are related to identities such as | |
| − | + | \begin{equation} \tag{a2} p ^ { - 1 } \prod _ { \underset{n \in \mathbf{Z} }{m > 0} } ( 1 - p ^ { m } q ^ { n } ) ^ { a_{ m n} } = j ( w ) - j ( z ) \end{equation} | |
| − | + | for $p = \operatorname { exp } ( 2 \pi i w )$, where $j ( z ) - 744 = \sum _ { k } a _ { k } q ^ { k }$, as well as to the existence of several modular equations obeyed by the $T_g$. These identities played a large role in the proof of moonshine. R. Borcherds proved that the $T_g$ obey (a1) by using the denominator identities of Borcherds algebras; the resulting modular equations can be used to prove the Hauptmodul property [[#References|[a7]]]. It would be very nice to see other direct connections between the group operation in $\bf M$ and the series $T_g$: for instance, are there other relations among the $T_g$ which correspond to more general products of conjugacy classes in $\bf M$? | |
| − | + | The Hirzebruch prize question [[#References|[a11]]] asks for a compact, differentiable, $24$-dimensional manifold on which $\bf M$ acts by diffeomorphisms and whose twisted Witten genus is $T_g$. It is still open (as of 2000). | |
| − | It still (as of 2000) is unclear why certain Hauptmoduls appear in moonshine and others do not. What form does moonshine (e.g. the replication formulas) take in genus | + | Vertex operator algebras are a key component in moonshine. There will be some form of moonshine for finite subgroups of the automorphism group of any rational vertex operator algebra obeying a technical (and probably redundant) "C2 condition" (see e.g. [[#References|[a18]]]). The resulting functions, however, will not be Hauptmoduls in general. There is no complete understanding yet (2000) of why Hauptmoduls are associated to $\bf M$, although it has been conjectured to do with the "6-transposition property" of $\bf M$ [[#References|[a12]]], or the uniqueness of $V ^ { \natural }$ [[#References|[a17]]]. |
| + | |||
| + | Moonshine is related to conformal field theory (e.g. $V ^ { \natural }$ is the chiral algebra of a holomorphic $c = 24$ theory), in which context many of moonshine's special features appear natural [[#References|[a8]]], [[#References|[a17]]], and this has motivated some of the developments (most significantly the definition of vertex operator algebras). | ||
| + | |||
| + | It still (as of 2000) is unclear why certain Hauptmoduls appear in moonshine and others do not. What form does moonshine (e.g. the replication formulas) take in genus $> 0$ (see e.g. [[#References|[a16]]])? How about moonshine for other groups (see e.g. [[#References|[a13]]])? In [[#References|[a14]]], a variant called modular moonshine was established, where $V ^ { \natural }$ is replaced with vertex algebras over characteristic $p$, and where the role of $\bf M$ is taken by centralizers in $\bf M$ of order $p$ elements. | ||
For his work in monstrous moonshine and related topics, Borcherds was awarded a Fields Medal in 1998 [[#References|[a5]]]. | For his work in monstrous moonshine and related topics, Borcherds was awarded a Fields Medal in 1998 [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. Alexander, C. Cummins, J. McKay, C. Simons, "Completely replicable functions" , ''Groups, Combinatorics and Geometry'' , Cambridge Univ. Press (1992) pp. 87–98</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R.E. Borcherds, "Vertex algebras, Kac–Moody algebras, and the Monster" ''Proc. Nat. Acad. Sci. USA'' , '''83''' (1986) pp. 3068–3071</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> R.E. Borcherds, "Generalized Kac–Moody algebras" ''J. Algebra'' , '''115''' (1988) pp. 501–512</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" ''Invent. Math.'' , '''109''' (1992) pp. 405–444</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R.E. Borcherds, "What is Moonshine?" , ''Proc. ICM, Berlin'' , DMV (1998) pp. 607–615</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> J.H. Conway, S.P. Norton, "Monstrous moonshine" ''Bull. London Math. Soc.'' , '''11''' (1979) pp. 308–339</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> C. Cummins, T. Gannon, "Modular equations and the genus $0$ property of Moonshine functions" ''Invent. Math.'' , '''129''' (1997) pp. 413–443</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> L. Dixon, P. Ginsparg, J. Harvey, "Beauty and the Beast: superconformal symmetry in a Monster module" ''Commun. Math. Phys.'' , '''119''' (1988) pp. 221–241</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operators and the monster" , Acad. Press (1988)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> R.L. Griess, "The friendly giant" ''Invent. Math.'' , '''69''' (1982) pp. 1–102</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> F. Hirzebruch, T. Berger, R. Jung, "Manifolds and modular forms" , ''Aspects of Math.'' , Vieweg (1994) (Edition: Second)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> S.P. Norton, "Generalized moonshine" ''Proc. Symp. Pure Math.'' , '''47''' (1987) pp. 208–209</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> L. Queen, "Modular functions arising from some finite groups" ''Math. Comput.'' , '''37''' (1981) pp. 547–580</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> A.J. E. Ryba, "Modular moonshine?" , ''Moonshine, the Monster, and Related Topics'' , ''Contemp. Math.'' , '''193''' , Amer. Math. Soc. (1996) pp. 307–336</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> R.E. Borcherds, "Modular moonshine III" ''Duke Math. J.'' , '''93''' (1998) pp. 129–154</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> G.W. Smith, "Replicant powers for higher genera" , ''Moonshine, the Monster, and Related Topics'' , ''Contemp. Math.'' , '''193''' , Amer. Math. Soc. (1996) pp. 337–352</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> M.P. Tuite, "On the relationship between Monstrous moonshine and the uniqueness of the Moonshine module" ''Commun. Math. Phys.'' , '''166''' (1995) pp. 495–532</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> Y. Zhu, "Modular invariance of characters of vertex operator algebras" ''J. Amer. Math. Soc.'' , '''9''' (1996) pp. 237–302</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> C. Dong, H. Li, G. Mason, "Modular invariance of trace functions in orbifold theory" ''preprint q-alg/9703016'' (1997)</td></tr></table> |
Revision as of 17:45, 1 July 2020
In 1978, J. McKay observed that $196884 = 196883 + 1$. The number on the left is the first non-trivial coefficient of the $j$-function, and the numbers on the right are the dimensions of the smallest irreducible representations of the Fischer–Griess Monster $\bf M$ [a10] (cf. also Sporadic simple group). On the one side stands a modular function; on the other, a finite sporadic simple group. Moonshine is the explanation and generalization of this unlikely connection.
Monstrous moonshine [a6] conjectured that there is an infinite-dimensional graded vector space $V = V _ { - 1 } \oplus V _ { 1 } \oplus V _ { 2 } \oplus \ldots$, with the following properties. Each $V _ { k }$ carries a finite-dimensional representation of $\bf M$; write $\chi _ { k }$ for its character. For each $g \in \mathbf{M}$, define the Thompson–McKay series $T _ { g } ( z ) = \sum _ { k = - 1 } ^ { \infty } \chi _ { k } ( g ) q ^ { k }$, where $q = \operatorname { exp } ( 2 \pi i z )$. Then $T_g$ is a generator ( "Hauptmodul" ) of the field of modular functions for some genus-$0$ group $G _ { g } \leq \operatorname {SL} _ { 2 } ( \mathbf{R} )$. The group $G _ { g }$ contains $\Gamma _ { 0 } ( N )$ as a normal subgroup, where $N$ divides $o ( g ) \operatorname { gcd } ( 24 , o ( g ) )$ ($o ( g )$ is the order of $g$).
There are $171$ distinct Thompson series ($\bf M$ has only $194$ conjugacy classes). For example, $G _ { e } = \operatorname{SL} _ { 2 } ( \mathbf{Z} )$ and $T _ { e } = j - 744$, where $e \in \mathbf{M}$ is the identity. $\bf M$ has two order-$2$ conjugacy classes, corresponding to the modular groups $\Gamma _ { 0 } ( 2 )$ and
\begin{equation*} \Gamma _ { 0 } ( 2 ) ^ { + } : = \left( \Gamma _ { 0 } ( 2 ) , \left( \begin{array} { c c } { 0 } & { - 1 } \\ { 2 } & { 0 } \end{array} \right) \right). \end{equation*}
Let $\rho _ { d }$ denote the $d$-dimensional irreducible representation of $\bf M$; then $V _ { - 1 } = \rho _ { 1 }$, $V _ { 1 } = \rho _ { 1 } \oplus \rho _ { 196883}$, and $V _ { 2 } = \rho _ { 1 } \oplus \rho _ { 196883 } \oplus \rho _ { 21296876 }$.
Central to these conjectures is the moonshine module $V ^ { \natural }$, constructed in [a9]. It is an important example of a vertex operator algebra (VOA) [a2], [a9], and as such possesses infinitely many heavily constrained bilinear products. One of these products makes $V _ { 1 }$ into the Griess algebra [a10] extended by an identity element. The automorphism group of $V ^ { \natural }$ is $\bf M$.
The monstrous moonshine conjectures, and, in particular, the identification of $V$ with $V ^ { \natural }$, were proved in [a4], which also defined vertex operator algebras and a generalization of Kac–Moody algebras called Borcherds or generalized Kac–Moody algebras [a3] (cf. also Kac–Moody algebra; Borcherds Lie algebra).
The series $T_g$ were generalized by S.P. Norton to commuting pairs $( g , h ) \in \bf M \times M$ [a12]. In particular, to each such pair there is a modular function $Z ( g,h ; z )$, invariant under a genus-$0$ group, such that
\begin{equation*} Z ( g ^ { a } h ^ { c } , g ^ { b } h ^ { d } ; z ) = \alpha Z \left( g ,h ; \frac { a z + b } { c z + d } \right) \end{equation*}
for some root of unity $\alpha$, for any
\begin{equation*} \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} _ { 2 } ( {\bf Z} ). \end{equation*}
This action of $\operatorname{SL} _ { 2 } ( \mathbf{Z} )$ is related to its natural action on the fundamental group $\mathbf{Z} ^ { 2 }$ of the torus. The coefficients of the $q$-expansion of $Z ( g,h ; z )$ are characters of the centralizer $C _ { \mathbf{M} } ( g )$ evaluated at $h$. Simultaneous conjugation of $g$, $h$ leaves $Z$ unchanged: $Z ( a g a ^ { - 1 } , a h a ^ { - 1 } ; z ) = Z ( g , h ; z )$. The Thompson–McKay series are recovered by the specialization $g = e$: $Z ( e , h ; z ) = T _ { h } ( z )$. Only special cases of these generalized moonshine conjectures have been proven.
There are several other conjectures. For example, the series $T _ { g ^ { i } }$ were conjecturally related by the replication formulas [a6], [a1]:
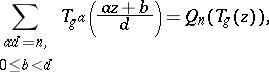 | (a1) |
where $Q _ { n }$ is the unique polynomial for which $Q _ { n } ( T _ { g } ( z ) ) - q ^ { - n }$ is a power series with only strictly positive powers of $q$. The resemblance of (a1) with Hecke operators is not accidental. These formulas are related to identities such as
\begin{equation} \tag{a2} p ^ { - 1 } \prod _ { \underset{n \in \mathbf{Z} }{m > 0} } ( 1 - p ^ { m } q ^ { n } ) ^ { a_{ m n} } = j ( w ) - j ( z ) \end{equation}
for $p = \operatorname { exp } ( 2 \pi i w )$, where $j ( z ) - 744 = \sum _ { k } a _ { k } q ^ { k }$, as well as to the existence of several modular equations obeyed by the $T_g$. These identities played a large role in the proof of moonshine. R. Borcherds proved that the $T_g$ obey (a1) by using the denominator identities of Borcherds algebras; the resulting modular equations can be used to prove the Hauptmodul property [a7]. It would be very nice to see other direct connections between the group operation in $\bf M$ and the series $T_g$: for instance, are there other relations among the $T_g$ which correspond to more general products of conjugacy classes in $\bf M$?
The Hirzebruch prize question [a11] asks for a compact, differentiable, $24$-dimensional manifold on which $\bf M$ acts by diffeomorphisms and whose twisted Witten genus is $T_g$. It is still open (as of 2000).
Vertex operator algebras are a key component in moonshine. There will be some form of moonshine for finite subgroups of the automorphism group of any rational vertex operator algebra obeying a technical (and probably redundant) "C2 condition" (see e.g. [a18]). The resulting functions, however, will not be Hauptmoduls in general. There is no complete understanding yet (2000) of why Hauptmoduls are associated to $\bf M$, although it has been conjectured to do with the "6-transposition property" of $\bf M$ [a12], or the uniqueness of $V ^ { \natural }$ [a17].
Moonshine is related to conformal field theory (e.g. $V ^ { \natural }$ is the chiral algebra of a holomorphic $c = 24$ theory), in which context many of moonshine's special features appear natural [a8], [a17], and this has motivated some of the developments (most significantly the definition of vertex operator algebras).
It still (as of 2000) is unclear why certain Hauptmoduls appear in moonshine and others do not. What form does moonshine (e.g. the replication formulas) take in genus $> 0$ (see e.g. [a16])? How about moonshine for other groups (see e.g. [a13])? In [a14], a variant called modular moonshine was established, where $V ^ { \natural }$ is replaced with vertex algebras over characteristic $p$, and where the role of $\bf M$ is taken by centralizers in $\bf M$ of order $p$ elements.
For his work in monstrous moonshine and related topics, Borcherds was awarded a Fields Medal in 1998 [a5].
References
| [a1] | D. Alexander, C. Cummins, J. McKay, C. Simons, "Completely replicable functions" , Groups, Combinatorics and Geometry , Cambridge Univ. Press (1992) pp. 87–98 |
| [a2] | R.E. Borcherds, "Vertex algebras, Kac–Moody algebras, and the Monster" Proc. Nat. Acad. Sci. USA , 83 (1986) pp. 3068–3071 |
| [a3] | R.E. Borcherds, "Generalized Kac–Moody algebras" J. Algebra , 115 (1988) pp. 501–512 |
| [a4] | R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" Invent. Math. , 109 (1992) pp. 405–444 |
| [a5] | R.E. Borcherds, "What is Moonshine?" , Proc. ICM, Berlin , DMV (1998) pp. 607–615 |
| [a6] | J.H. Conway, S.P. Norton, "Monstrous moonshine" Bull. London Math. Soc. , 11 (1979) pp. 308–339 |
| [a7] | C. Cummins, T. Gannon, "Modular equations and the genus $0$ property of Moonshine functions" Invent. Math. , 129 (1997) pp. 413–443 |
| [a8] | L. Dixon, P. Ginsparg, J. Harvey, "Beauty and the Beast: superconformal symmetry in a Monster module" Commun. Math. Phys. , 119 (1988) pp. 221–241 |
| [a9] | I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operators and the monster" , Acad. Press (1988) |
| [a10] | R.L. Griess, "The friendly giant" Invent. Math. , 69 (1982) pp. 1–102 |
| [a11] | F. Hirzebruch, T. Berger, R. Jung, "Manifolds and modular forms" , Aspects of Math. , Vieweg (1994) (Edition: Second) |
| [a12] | S.P. Norton, "Generalized moonshine" Proc. Symp. Pure Math. , 47 (1987) pp. 208–209 |
| [a13] | L. Queen, "Modular functions arising from some finite groups" Math. Comput. , 37 (1981) pp. 547–580 |
| [a14] | A.J. E. Ryba, "Modular moonshine?" , Moonshine, the Monster, and Related Topics , Contemp. Math. , 193 , Amer. Math. Soc. (1996) pp. 307–336 |
| [a15] | R.E. Borcherds, "Modular moonshine III" Duke Math. J. , 93 (1998) pp. 129–154 |
| [a16] | G.W. Smith, "Replicant powers for higher genera" , Moonshine, the Monster, and Related Topics , Contemp. Math. , 193 , Amer. Math. Soc. (1996) pp. 337–352 |
| [a17] | M.P. Tuite, "On the relationship between Monstrous moonshine and the uniqueness of the Moonshine module" Commun. Math. Phys. , 166 (1995) pp. 495–532 |
| [a18] | Y. Zhu, "Modular invariance of characters of vertex operator algebras" J. Amer. Math. Soc. , 9 (1996) pp. 237–302 |
| [a19] | C. Dong, H. Li, G. Mason, "Modular invariance of trace functions in orbifold theory" preprint q-alg/9703016 (1997) |
Moonshine conjectures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moonshine_conjectures&oldid=18566