Monotone operator
One of the notions in non-linear functional analysis.
Let  be a Banach space,
be a Banach space, 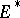 its dual, and let
its dual, and let  be the value of a linear functional
be the value of a linear functional 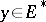 at an element
at an element 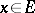 . An operator
. An operator 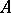 , in general non-linear and acting from
, in general non-linear and acting from 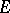 into
into 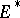 , is called monotone if
, is called monotone if
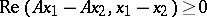 | (1) |
for any  . An operator
. An operator 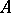 is called semi-continuous if for any
is called semi-continuous if for any 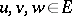 the numerical function
the numerical function 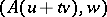 is continuous in
is continuous in 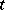 . An example of a semi-continuous monotone operator is the gradient of a convex Gâteaux-differentiable functional. Many functionals in variational calculus are convex and hence generate monotone operators; they are useful in the solution of non-linear integral equations and were in fact first applied there.
. An example of a semi-continuous monotone operator is the gradient of a convex Gâteaux-differentiable functional. Many functionals in variational calculus are convex and hence generate monotone operators; they are useful in the solution of non-linear integral equations and were in fact first applied there.
Various applications of monotone operators in questions regarding the solvability of non-linear equations are based on the following theorem (see [1], [2]). Let 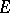 be a reflexive Banach space (cf. Reflexive space) and let
be a reflexive Banach space (cf. Reflexive space) and let  be a semi-continuous monotone operator with the property of coerciveness:
be a semi-continuous monotone operator with the property of coerciveness:
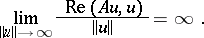 |
Then for any 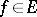 the equation
the equation  has at least one solution.
has at least one solution.
An operator 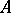 defined on a set
defined on a set 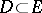 with values in
with values in  is called monotone on
is called monotone on 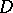 if (1) holds for any
if (1) holds for any 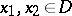 , and it is called maximal monotone if it is monotone on
, and it is called maximal monotone if it is monotone on  and has no monotone proper (strict) extension.
and has no monotone proper (strict) extension.
Research into equations with monotone operators has been stimulated to a large extent by problems in the theory of quasi-linear elliptic and parabolic equations. For example, boundary value problems for quasi-linear parabolic equations lead to equations of the form
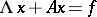 | (2) |
in a suitable Banach space  . The same equation also arises naturally in the investigation of the Cauchy problem for an abstract evolution equation with a non-linear operator in Banach spaces. If
. The same equation also arises naturally in the investigation of the Cauchy problem for an abstract evolution equation with a non-linear operator in Banach spaces. If 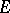 is reflexive and
is reflexive and 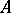 is a bounded, semi-continuous and coercive operator with dense domain of definition in
is a bounded, semi-continuous and coercive operator with dense domain of definition in  , then (2) is solvable for any
, then (2) is solvable for any 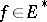 . The idea of monotonicity has also been applied in the problem of almost-periodic solutions of non-linear parabolic equations.
. The idea of monotonicity has also been applied in the problem of almost-periodic solutions of non-linear parabolic equations.
References
| [1] | F. Browder, "Non-linear parabolic boundary value problems of arbitrary order" Bull. Amer. Math. Soc. , 69 (1963) pp. 858–861 |
| [2] | G.J. Minty, "On a "monotonicity" method for the solution of non-linear problems in Banach spaces" Proc. Nat. Acad. Sci. USA , 50 (1963) pp. 1038–1041 |
| [3] | M.M. Vainberg, R.I. Kachurovskii, "On the variational theory of non-linear operators and equations" Dokl. Akad. Nauk SSSR , 129 : 6 (1959) pp. 1199–1202 (In Russian) |
| [4] | M.M. Vainberg, "Variational method and method of monotone operators in the theory of nonlinear equations" , Wiley (1973) (Translated from Russian) |
| [5] | J.-L. Lions, "Quelques méthodes de résolution des problèmes aux limites nonlineaires" , Dunod (1969) |
| [6] | B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian) |
| [7] | R.I. Kachurovskii, "Nonlinear monotone operators in Banach spaces" Russian Math. Surveys , 23 : 2 (1968) pp. 117–165 Uspekhi Mat. Nauk , 23 : 2 (1968) pp. 121–168 |
Monotone operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monotone_operator&oldid=17574