Monoidal transformation
blowing up,  -process
-process
A special kind of birational morphism of an algebraic variety or bimeromorphic morphism of an analytic space. For example, let  be an algebraic variety (or an arbitrary scheme), and let
be an algebraic variety (or an arbitrary scheme), and let  be a closed subvariety given by a sheaf of ideals
be a closed subvariety given by a sheaf of ideals  . The monoidal transformation of
. The monoidal transformation of  with centre
with centre  is the
is the  -scheme
-scheme  — the projective spectrum of the graded sheaf of
— the projective spectrum of the graded sheaf of 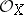 -algebras
-algebras 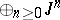 . If
. If 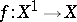 is the structure morphism of the
is the structure morphism of the  -scheme
-scheme 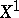 , then the sheaf of ideals
, then the sheaf of ideals 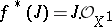 on
on  (defining the exceptional subscheme
(defining the exceptional subscheme 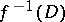 on
on 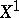 ) is invertible. This means that
) is invertible. This means that 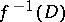 is a divisor on
is a divisor on 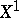 ; in addition,
; in addition, 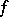 induces an isomorphism between
induces an isomorphism between  and
and  . A monoidal transformation
. A monoidal transformation  of a scheme
of a scheme 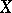 with centre
with centre 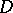 is characterized by the following universal property [1]: The sheaf of ideals
is characterized by the following universal property [1]: The sheaf of ideals  is invertible and for any morphism
is invertible and for any morphism 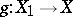 for which
for which  is invertible there is a unique morphism
is invertible there is a unique morphism 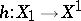 such that
such that 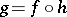 .
.
A monoidal transformation of an algebraic or analytic space 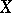 with as centre a closed subspace
with as centre a closed subspace 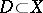 can be defined and characterized in the same way.
can be defined and characterized in the same way.
An important class of monoidal transformations are the admissible monoidal transformations, which are distinguished by the condition that  is non-singular and
is non-singular and  is a normally flat scheme along
is a normally flat scheme along 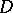 . The latter means that all sheaves
. The latter means that all sheaves  are flat
are flat 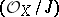 -modules. The importance of admissible monoidal transformations is explained by the fact that they do not worsen the singularities of the variety. In addition, it has been proved (see [1]) that a suitable sequence of admissible monoidal transformations improves singularities, which allows one to prove the theorem on the resolution of singularities for an algebraic variety over a field of characteristic zero.
-modules. The importance of admissible monoidal transformations is explained by the fact that they do not worsen the singularities of the variety. In addition, it has been proved (see [1]) that a suitable sequence of admissible monoidal transformations improves singularities, which allows one to prove the theorem on the resolution of singularities for an algebraic variety over a field of characteristic zero.
Admissible monoidal transformations of non-singular varieties are particularly simple to construct. If  is a monoidal transformation with a non-singular centre
is a monoidal transformation with a non-singular centre  , then
, then 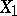 is again non-singular and the exceptional subspace
is again non-singular and the exceptional subspace 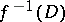 is canonically isomorphic to the projectivization of the conormal sheaf to
is canonically isomorphic to the projectivization of the conormal sheaf to 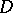 in
in  . In the special case when
. In the special case when 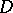 consists of one point, the monoidal transformation consists of blowing up this point into the whole projective space of tangent directions. For the behaviour of various invariants of non-singular varieties (such as Chow rings, cohomology spaces, the
consists of one point, the monoidal transformation consists of blowing up this point into the whole projective space of tangent directions. For the behaviour of various invariants of non-singular varieties (such as Chow rings, cohomology spaces, the  -functor, and Chern classes) under admissible monoidal transformations see [2]–[5].
-functor, and Chern classes) under admissible monoidal transformations see [2]–[5].
References
| [1] | H. Hironaka, "Resolution of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. (2) , 79 (1964) pp. 109–326 |
| [2] | P. Berthelot (ed.) A. Grothendieck (ed.) L. Illusie (ed.) et al. (ed.) , Théorie des intersections et théorème de Riemann–Roch (SGA 6) , Lect. notes in math. , 225 , Springer (1971) |
| [3] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie  -adique et fonctions -adique et fonctions 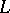 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) . SGA 5" , Lect. notes in math. , 589 , Springer (1977) |
| [4] | I. Porteous, "Blowing up Chern classes" Proc. Cambridge Philos. Soc. , 56 : 2 (1960) pp. 118–124 |
| [5] | Yu.I. Manin, "Lectures on the 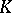 -functor in algebraic geometry" Russian Math. Surveys , 24 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 -functor in algebraic geometry" Russian Math. Surveys , 24 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 |
Comments
The word "s-process" appeared for the first time in [a1].
References
| [a1] | H. Hopf, "Schlichte Abbildungen und lokale Modifikationen 4-dimensionaler komplexer Mannigfaltigkeiten" Comm. Math. Helv. , 29 (1954) pp. 132–156 |
Monoidal transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monoidal_transformation&oldid=13914