Monoid
A term used as an abbreviation for the phrase "semi-group with identity" . Thus, a monoid is a set 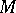 with an associative binary operation, usually called multiplication, in which there is an element
with an associative binary operation, usually called multiplication, in which there is an element  such that
such that 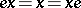 for any
for any 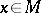 . The element
. The element  is called the identity (or unit) and is usually denoted by
is called the identity (or unit) and is usually denoted by 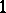 . In any monoid there is exactly one identity. If the operation given on the monoid is commutative, it is often called addition and the identity is called the zero and is denoted by
. In any monoid there is exactly one identity. If the operation given on the monoid is commutative, it is often called addition and the identity is called the zero and is denoted by  .
.
Examples of monoids. 1) The set of all mappings of an arbitrary set 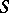 into itself is a monoid relative to the operation of successive application (composition) of mappings. The identity mapping is the identity. 2) The set of endomorphisms of a universal algebra
into itself is a monoid relative to the operation of successive application (composition) of mappings. The identity mapping is the identity. 2) The set of endomorphisms of a universal algebra 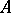 is a monoid relative to composition; the identity is the identity endomorphism. 3) Every group is a monoid.
is a monoid relative to composition; the identity is the identity endomorphism. 3) Every group is a monoid.
Every semi-group 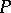 without an identity can be imbedded in a monoid. For this it suffices to take a symbol
without an identity can be imbedded in a monoid. For this it suffices to take a symbol 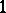 not in
not in 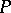 and give a multiplication on the set
and give a multiplication on the set 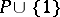 as follows:
as follows: 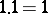 ,
, 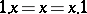 for any
for any 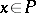 , and on elements from
, and on elements from 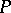 the operation is as before. Every monoid can be represented as the monoid of all endomorphisms of some universal algebra.
the operation is as before. Every monoid can be represented as the monoid of all endomorphisms of some universal algebra.
An arbitrary monoid can also be considered as a category with one object. This allows one to associate with a monoid 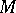 its dual (opposite, adjoint) monoid
its dual (opposite, adjoint) monoid 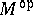 . The elements of both monoids coincide, but the product of
. The elements of both monoids coincide, but the product of  and
and 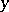 in
in 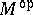 is put equal to the product
is put equal to the product  in
in 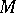 .
.
The development of the theory of monoids and adjoint functors has shown the utility of the definition of a monoid in so-called monoidal categories. Suppose given a category 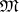 equipped with a bifunctor
equipped with a bifunctor 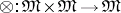 , an object
, an object 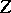 and natural isomorphisms
and natural isomorphisms
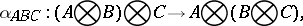 |
 |
satisfying coherence conditions. An object 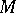 is called a monoid in the category
is called a monoid in the category  if there are morphisms
if there are morphisms 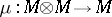 and
and 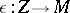 such that the following diagrams are commutative:
such that the following diagrams are commutative:
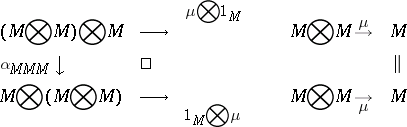 |
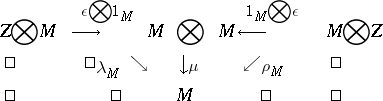 |
If 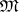 is taken to be the category of sets (cf. Sets, category of),
is taken to be the category of sets (cf. Sets, category of),  the Cartesian product,
the Cartesian product,  a one-point set, and the isomorphisms
a one-point set, and the isomorphisms 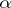 ,
, 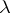 and
and 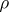 are chosen in the natural way (
are chosen in the natural way (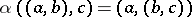 ,
, 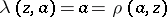 ), then the second definition of a monoid turns out to be equivalent to the original definition.
), then the second definition of a monoid turns out to be equivalent to the original definition.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
Comments
For monoidal categories, and particularly the coherence conditions that the isomorphisms 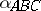 ,
,  must satisfy cf. [1], Chapt. 7, Sects. 1-2.
must satisfy cf. [1], Chapt. 7, Sects. 1-2.
Monoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monoid&oldid=18430