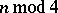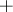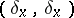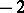Monodromy transformation
A transformation of the fibres (or of their homotopy invariants) of a fibre space corresponding to a path in the base. More precisely, let 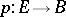 be a locally trivial fibre space and let
be a locally trivial fibre space and let 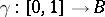 be a path in
be a path in 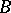 with initial point
with initial point 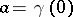 and end-point
and end-point 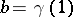 . A trivialization of the fibration
. A trivialization of the fibration 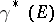 defines a homeomorphism
defines a homeomorphism 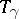 of the fibre
of the fibre 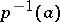 onto the fibre
onto the fibre 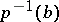 ,
, 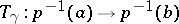 . If the trivialization of
. If the trivialization of 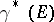 is modified, then
is modified, then 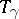 changes into a homotopically-equivalent homeomorphism; this also happens if
changes into a homotopically-equivalent homeomorphism; this also happens if 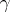 is changed to a homotopic path. The homotopy type of
is changed to a homotopic path. The homotopy type of 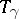 is called the monodromy transformation corresponding to a path
is called the monodromy transformation corresponding to a path 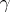 . When
. When 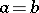 , that is, when
, that is, when 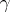 is a loop, the monodromy transformation
is a loop, the monodromy transformation 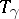 is a homeomorphism of
is a homeomorphism of 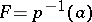 into itself (defined, yet again, up to a homotopy). This mapping, and also the homomorphisms induced by it on the homology and cohomology spaces of
into itself (defined, yet again, up to a homotopy). This mapping, and also the homomorphisms induced by it on the homology and cohomology spaces of 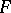 , is also called a monodromy transformation. The correspondence of
, is also called a monodromy transformation. The correspondence of 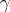 with
with 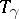 gives a representation of the fundamental group
gives a representation of the fundamental group 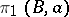 on
on 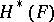 .
.
The idea of a monodromy transformation arose in the study of multi-valued functions (see Monodromy theorem). If 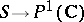 is the Riemann surface of such a function, then by eliminating the singular points of the function from the Riemann sphere
is the Riemann surface of such a function, then by eliminating the singular points of the function from the Riemann sphere  , an unbranched covering is obtained. The monodromy transformation in this case is also called a covering or deck transformation.
, an unbranched covering is obtained. The monodromy transformation in this case is also called a covering or deck transformation.
The monodromy transformation arises most frequently in the following situation. Let 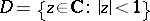 be the unit disc in the complex plane, let
be the unit disc in the complex plane, let 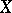 be an analytic space, let
be an analytic space, let 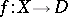 be a proper holomorphic mapping (cf. Proper morphism), let
be a proper holomorphic mapping (cf. Proper morphism), let 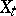 be the fibre
be the fibre 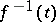 ,
, 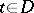 ,
, 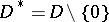 , and let
, and let 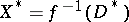 . Diminishing, if necessary, the radius of
. Diminishing, if necessary, the radius of 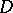 , the fibre space
, the fibre space 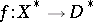 can be made locally trivial. The monodromy transformation
can be made locally trivial. The monodromy transformation 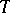 associated with a circuit around
associated with a circuit around  in
in 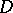 is called the monodromy of the family
is called the monodromy of the family 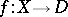 at
at 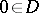 , it acts on the (co)homology spaces of the fibre
, it acts on the (co)homology spaces of the fibre 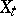 , where
, where  . The most studied case is when
. The most studied case is when 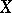 and the fibres
and the fibres 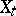 ,
, 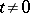 , are smooth. The action of
, are smooth. The action of 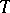 on
on 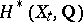 , in this case, is quasi-unipotent [4], that is, there are positive integers
, in this case, is quasi-unipotent [4], that is, there are positive integers 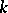 and
and 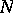 such that
such that 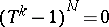 . The properties of the monodromy display many characteristic features of the degeneracy of the family
. The properties of the monodromy display many characteristic features of the degeneracy of the family 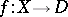 . The monodromy of the family
. The monodromy of the family 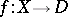 is closely related to mixed Hodge structures (cf. Hodge structure) on the cohomology spaces
is closely related to mixed Hodge structures (cf. Hodge structure) on the cohomology spaces 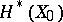 and
and 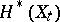 (see [5]–[7]).
(see [5]–[7]).
When the singularities of 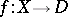 are isolated, the monodromy transformation can be localized. Let
are isolated, the monodromy transformation can be localized. Let  be a singular point of
be a singular point of 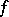 (or, equivalently, of
(or, equivalently, of 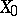 ) and let
) and let 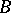 be a sphere of sufficiently small radius in
be a sphere of sufficiently small radius in 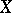 with centre at
with centre at  . Diminishing, if necessary, the radius of
. Diminishing, if necessary, the radius of 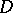 , a local trivialization of the fibre space
, a local trivialization of the fibre space 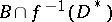 can be defined. It is compatible with the trivialization of the fibre space
can be defined. It is compatible with the trivialization of the fibre space 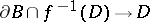 on the boundary. This gives a diffeomorphism
on the boundary. This gives a diffeomorphism 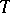 of the manifold of "vanishing cycles"
of the manifold of "vanishing cycles" 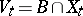 into itself which is the identity on
into itself which is the identity on 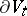 , and which is called the local monodromy of
, and which is called the local monodromy of 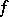 at
at  . The action of the monodromy transformation on the cohomology spaces
. The action of the monodromy transformation on the cohomology spaces 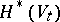 reflects the singularity of
reflects the singularity of 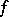 at
at  (see [1], [2], [7]). It is known that the manifold
(see [1], [2], [7]). It is known that the manifold 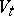 is homotopically equivalent to a bouquet of
is homotopically equivalent to a bouquet of 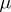
 -dimensional spheres, where
-dimensional spheres, where 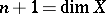 and
and 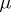 is the Milnor number of the germ of
is the Milnor number of the germ of 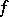 at
at  .
.
The simplest case is that of a Morse singularity when, in a neighbourhood of  ,
, 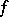 reduces to the form
reduces to the form 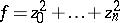 (cf. Morse lemma). In this case
(cf. Morse lemma). In this case 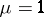 , and the interior
, and the interior 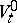 of
of 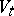 is diffeomorphic to the tangent bundle of the
is diffeomorphic to the tangent bundle of the  -dimensional sphere
-dimensional sphere 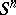 . A vanishing cycle
. A vanishing cycle 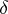 is a generator of the cohomology group with compact support
is a generator of the cohomology group with compact support 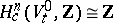 , defined up to sign. In general, if
, defined up to sign. In general, if 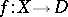 is a proper holomorphic mapping (as above, having a unique Morse singularity at
is a proper holomorphic mapping (as above, having a unique Morse singularity at  ), then a cycle
), then a cycle 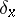 vanishing at
vanishing at  is the image of a cycle
is the image of a cycle 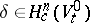 under the natural mapping
under the natural mapping 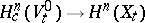 . In this case the specialization homomorphism
. In this case the specialization homomorphism 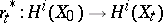 is an isomorphism for
is an isomorphism for 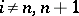 , and the sequence
, and the sequence
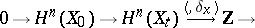 |
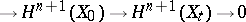 |
is exact. The monodromy transformation 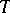 acts trivially on
acts trivially on 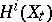 for
for 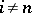 and its action on
and its action on  is given by the Picard–Lefschetz formula: For
is given by the Picard–Lefschetz formula: For 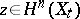 ,
,
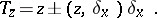 |
The sign in this formula and the values of 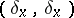 are collected in the table.'
are collected in the table.'
<tbody> </tbody>
|
A monodromy transformation preserves the intersection form on 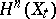 .
.
Vanishing cycles and monodromy transformations are used in the Picard–Lefschetz theory, associating the cohomology space of a projective complex manifold and its hyperplane sections. Let 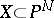 be a smooth manifold of dimension
be a smooth manifold of dimension 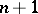 , and let
, and let 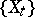 ,
, 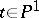 , be a pencil of hyperplane sections of
, be a pencil of hyperplane sections of 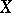 with basic set (axis of the pencil)
with basic set (axis of the pencil) 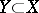 ; let the following conditions be satisfied: a)
; let the following conditions be satisfied: a) 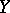 is a smooth submanifold in
is a smooth submanifold in 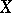 ; b) there is a finite set
; b) there is a finite set 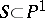 such that
such that 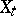 is smooth for
is smooth for 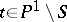 ; and c) for
; and c) for 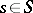 the manifold
the manifold 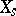 has a unique non-degenerate quadratic singular point
has a unique non-degenerate quadratic singular point 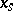 , where
, where 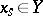 . Pencils with these properties (Lefschetz pencils) always exist. Let
. Pencils with these properties (Lefschetz pencils) always exist. Let 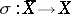 be a monoidal transformation with centre on the axis
be a monoidal transformation with centre on the axis 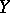 of the pencil, and let
of the pencil, and let 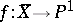 be the morphism defined by the pencil
be the morphism defined by the pencil 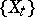 ; here
; here 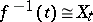 for all
for all 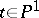 . Let a point
. Let a point 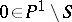 be fixed; then the monodromy transformation gives an action of
be fixed; then the monodromy transformation gives an action of 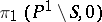 on
on 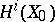 (non-trivial only for
(non-trivial only for 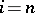 ). To describe the action of the monodromy on
). To describe the action of the monodromy on 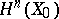 one chooses points
one chooses points 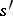 , situated near
, situated near 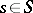 , and paths
, and paths 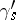 leading from
leading from  to
to 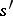 . Let
. Let 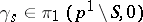 be the loop constructed as follows: first go along
be the loop constructed as follows: first go along 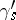 , then once round
, then once round  and, finally, return along
and, finally, return along 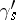 to
to  . In addition, let
. In addition, let 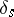 be a cycle vanishing at
be a cycle vanishing at 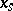 (more precisely, take a vanishing cycle in
(more precisely, take a vanishing cycle in 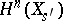 and transfer it to
and transfer it to 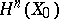 by means of the monodromy transformation corresponding to the path
by means of the monodromy transformation corresponding to the path 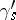 ). Finally, let
). Finally, let 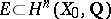 be the subspace generated by the vanishing cycles
be the subspace generated by the vanishing cycles 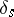 ,
, 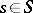 (the vanishing cohomology space). Then the following hold.
(the vanishing cohomology space). Then the following hold.
1) 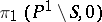 is generated by the elements
is generated by the elements 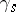 ,
, 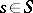 ;
;
2) the action of 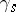 is given by the formula
is given by the formula
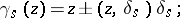 |
3) the space 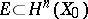 is invariant under the action of the monodromy group
is invariant under the action of the monodromy group 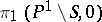 ;
;
4) the space of elements in 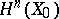 that are invariant relative to monodromy coincides with the orthogonal complement of
that are invariant relative to monodromy coincides with the orthogonal complement of 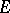 relative to the intersection form on
relative to the intersection form on 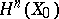 , and also with the images of the natural homomorphisms
, and also with the images of the natural homomorphisms 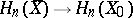 and
and 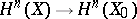 ;
;
5) the vanishing cycles 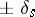 are conjugate (up to sign) under the action of
are conjugate (up to sign) under the action of 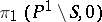 ;
;
6) the action of 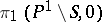 on
on 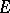 is absolutely irreducible.
is absolutely irreducible.
The formalism of vanishing cycles, monodromy transformations and the Picard–Lefschetz theory has also been constructed for 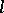 -adic cohomology spaces of algebraic varieties over any field (see [3]).
-adic cohomology spaces of algebraic varieties over any field (see [3]).
References
| [1] | V.I. Arnol'd, "Normal forms of functions in neighbourhoods of degenerate critical points" Russian Math. Surveys , 29 : 2 (1974) pp. 10–50 Uspekhi Mat. Nauk , 29 : 2 (1974) pp. 11–49 |
| [2] | J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) |
| [3] | P. Deligne (ed.) N.M. Katz (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) |
| [4] | C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" Trans. Amer. Math. Soc. , 136 (1969) pp. 93–108 |
| [5] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 |
| [6] | J. Steenbrink, "Limits of Hodge structures" Invent. Math. , 31 (1976) pp. 229–257 |
| [7] | J.H.M. Steenbrink, "Mixed Hodge structure on the vanishing cohomology" P. Holm (ed.) , Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School , Sijthoff & Noordhoff (1977) pp. 524–563 |
| [8] | S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) |
| [9] | S. Lefschetz, "A page of mathematical autobiography" Bull. Amer. Math. Soc. , 74 : 5 (1968) pp. 854–879 |
Monodromy transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monodromy_transformation&oldid=18530