Modulus of an elliptic integral
From Encyclopedia of Mathematics
The parameter  which enters into the expression of the elliptic integral in Legendre normal form. For example, in the incomplete elliptic integral of the first kind,
which enters into the expression of the elliptic integral in Legendre normal form. For example, in the incomplete elliptic integral of the first kind,
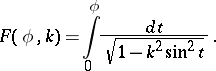 | (*) |
The number  is sometimes called the Legendre modulus,
is sometimes called the Legendre modulus,  is called the complementary modulus. In applications the normal case
is called the complementary modulus. In applications the normal case  usually holds; here the sharp angle
usually holds; here the sharp angle  for which
for which  is called the modular angle. The modulus
is called the modular angle. The modulus  also enters into the expression of the Jacobi elliptic functions, which arise from the inversion of elliptic integrals of the form (*).
also enters into the expression of the Jacobi elliptic functions, which arise from the inversion of elliptic integrals of the form (*).
Comments
References
| [a1] | F. Bowman, "Introduction to elliptic functions with applications" , Dover, reprint (1961) |
How to Cite This Entry:
Modulus of an elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modulus_of_an_elliptic_integral&oldid=15159
Modulus of an elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modulus_of_an_elliptic_integral&oldid=15159
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article