Difference between revisions of "Modular group"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47871 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644401.png" /> of all fractional-linear transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644402.png" /> of the form |
| − | m0644401.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644403.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | The group | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644404.png" /> are rational integers. The modular group can be identified with the quotient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644405.png" />, where |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644406.png" /></td> </tr></table> | |
| − | |||
| − | + | and is a [[Discrete subgroup|discrete subgroup]] in the [[Lie group|Lie group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644407.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644408.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m0644409.png" />) is the group of matrices | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444010.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444011.png" /> real numbers (respectively, integers) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444012.png" />. The modular group is a [[Discrete group of transformations|discrete group of transformations]] of the complex upper half-plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444013.png" /> (sometimes called the Lobachevskii plane or Poincaré upper half-plane) and has a presentation with generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444015.png" />, and relations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444016.png" />, that is, it is the free product of the cyclic group of order 2 generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444017.png" /> and the cyclic group of order 3 generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444018.png" /> (see [[#References|[2]]]). | |
| − | |||
| − | + | Interest in the modular group is related to the study of modular functions (cf. [[Modular function|Modular function]]) whose Riemann surfaces (cf. [[Riemann surface|Riemann surface]]) are quotient spaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444019.png" />, identified with a fundamental domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444020.png" /> of the modular group. The compactification <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444021.png" /> is analytically isomorphic to the complex projective line, where the isomorphism is given by the fundamental modular function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444022.png" />. The fundamental domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444023.png" /> has finite Lobachevskii area: | |
| − | |||
| − | |||
| − | is the | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444024.png" /></td> </tr></table> | |
| − | |||
| − | + | that is, the modular group is a [[Fuchsian group|Fuchsian group]] of the first kind (see [[#References|[3]]]). For the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444026.png" />, the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444027.png" />, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | see [[#References|[ | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444028.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444029.png" />, that is, can be obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444030.png" /> by multiplying the elements of the latter by a non-zero complex number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444031.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444032.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | that is | + | Corresponding to each lattice there is a complex torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444033.png" /> that is analytically equivalent to a non-singular cubic curve (an [[Elliptic curve|elliptic curve]]). This gives a one-to-one correspondence between the points of the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444034.png" />, classes of equivalent lattices and the classes of (analytically) equivalent elliptic curves (see [[#References|[3]]]). |
| − | |||
| − | |||
| − | + | The investigation of the subgroups of the modular group is of interest in the theory of modular forms and algebraic curves (cf. [[Algebraic curve|Algebraic curve]]; [[Modular form|Modular form]]). The principal congruence subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444036.png" /> of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444037.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444038.png" /> an integer) is the group of transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444039.png" /> of the form (1) for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444040.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444041.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444042.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444043.png" />). A subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444044.png" /> is called a congruence subgroup if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444045.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444046.png" />; the least such <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444047.png" /> is called the level of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444048.png" />. Examples of congruence subgroups of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444049.png" /> are: the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444050.png" /> of transformations (1) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444051.png" /> divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444052.png" />, and the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444053.png" /> of transformations (1) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444054.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444055.png" />) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444056.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444057.png" />). The [[Index|index]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444058.png" /> in the modular group is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444059.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444061.png" /> is a prime number, and 6 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444062.png" />; thus, each congruence subgroup has finite index in the modular group. | |
| − | |||
| − | |||
| − | + | Corresponding to each subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444063.png" /> of finite index in the modular group there is a complete algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444064.png" /> (a [[Modular curve|modular curve]]), obtained from the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444065.png" /> and the covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444066.png" />. The study of the branches of this covering allows one to find generators and relations for the congruence subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444067.png" />, the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064440/m06444068.png" /> and to prove that there are subgroups of finite index in the modular group which are not congruence subgroups (see [[#References|[3]]], [[#References|[8]]], [[#References|[7]]], Vol. 2). The study of presentations of the modular group was initiated in work (see [[#References|[4]]], [[#References|[6]]]) connected with the theory of modular forms. Such presentations were intensively studied within the theory of automorphic forms (see [[#References|[7]]] and [[Automorphic form|Automorphic form]]). Many results related to the modular group have been transferred to the case of arithmetic subgroups of algebraic Lie groups (cf. [[Arithmetic group|Arithmetic group]]; [[Lie algebra, algebraic|Lie algebra, algebraic]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Corresponding to each | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | of finite index in the modular group there is a complete algebraic curve | ||
| − | a [[Modular curve|modular curve]]), obtained from the quotient space | ||
| − | and the covering | ||
| − | The study of the branches of this covering allows one to find generators and relations for the congruence subgroup | ||
| − | the genus of | ||
| − | and to prove that there are subgroups of finite index in the modular group which are not congruence subgroups (see [[#References|[3]]], [[#References|[8]]], [[#References|[7]]], Vol. 2). The study of presentations of the modular group was initiated in work (see [[#References|[4]]], [[#References|[6]]]) connected with the theory of modular forms. Such presentations were intensively studied within the theory of automorphic forms (see [[#References|[7]]] and [[Automorphic form|Automorphic form]]). Many results related to the modular group have been transferred to the case of arithmetic subgroups of algebraic Lie groups (cf. [[Arithmetic group|Arithmetic group]]; [[Lie algebra, algebraic|Lie algebra, algebraic]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) pp. Chapt.8</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Hecke, "Analytische Arithmetik der positiven quadratischen Formen" , ''Mathematische Werke'' , Vandenhoeck & Ruprecht (1959) pp. 789–918</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , '''1–2''' , Teubner (1890–1892)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H.D. Kloosterman, "The behaviour of general theta functions under the modular group and the characters of binary modular congruence groups I, II" ''Ann. of Math.'' , '''47''' (1946) pp. 317–375; 376–417</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) pp. Chapt.8</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Hecke, "Analytische Arithmetik der positiven quadratischen Formen" , ''Mathematische Werke'' , Vandenhoeck & Ruprecht (1959) pp. 789–918</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , '''1–2''' , Teubner (1890–1892)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> H.D. Kloosterman, "The behaviour of general theta functions under the modular group and the characters of binary modular congruence groups I, II" ''Ann. of Math.'' , '''47''' (1946) pp. 317–375; 376–417</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977)</TD></TR></table> | ||
Revision as of 13:51, 7 June 2020
The group 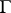 of all fractional-linear transformations
of all fractional-linear transformations 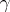 of the form
of the form
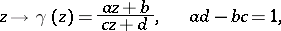 | (1) |
where 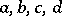 are rational integers. The modular group can be identified with the quotient group
are rational integers. The modular group can be identified with the quotient group 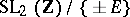 , where
, where
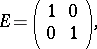 |
and is a discrete subgroup in the Lie group 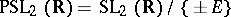 . Here
. Here 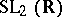 (respectively,
(respectively, 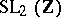 ) is the group of matrices
) is the group of matrices
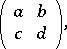 |
with 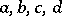 real numbers (respectively, integers) and
real numbers (respectively, integers) and 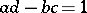 . The modular group is a discrete group of transformations of the complex upper half-plane
. The modular group is a discrete group of transformations of the complex upper half-plane 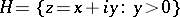 (sometimes called the Lobachevskii plane or Poincaré upper half-plane) and has a presentation with generators
(sometimes called the Lobachevskii plane or Poincaré upper half-plane) and has a presentation with generators 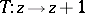 and
and 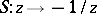 , and relations
, and relations 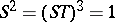 , that is, it is the free product of the cyclic group of order 2 generated by
, that is, it is the free product of the cyclic group of order 2 generated by 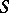 and the cyclic group of order 3 generated by
and the cyclic group of order 3 generated by 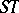 (see [2]).
(see [2]).
Interest in the modular group is related to the study of modular functions (cf. Modular function) whose Riemann surfaces (cf. Riemann surface) are quotient spaces of 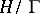 , identified with a fundamental domain
, identified with a fundamental domain 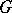 of the modular group. The compactification
of the modular group. The compactification 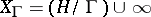 is analytically isomorphic to the complex projective line, where the isomorphism is given by the fundamental modular function
is analytically isomorphic to the complex projective line, where the isomorphism is given by the fundamental modular function 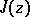 . The fundamental domain
. The fundamental domain 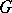 has finite Lobachevskii area:
has finite Lobachevskii area:
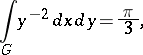 |
that is, the modular group is a Fuchsian group of the first kind (see [3]). For the lattice 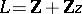 ,
, 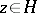 , the lattice
, the lattice 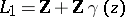 ,
,
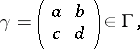 |
is equivalent to 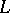 , that is, can be obtained from
, that is, can be obtained from 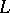 by multiplying the elements of the latter by a non-zero complex number
by multiplying the elements of the latter by a non-zero complex number 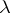 ,
, 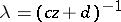 .
.
Corresponding to each lattice there is a complex torus 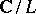 that is analytically equivalent to a non-singular cubic curve (an elliptic curve). This gives a one-to-one correspondence between the points of the quotient space
that is analytically equivalent to a non-singular cubic curve (an elliptic curve). This gives a one-to-one correspondence between the points of the quotient space 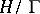 , classes of equivalent lattices and the classes of (analytically) equivalent elliptic curves (see [3]).
, classes of equivalent lattices and the classes of (analytically) equivalent elliptic curves (see [3]).
The investigation of the subgroups of the modular group is of interest in the theory of modular forms and algebraic curves (cf. Algebraic curve; Modular form). The principal congruence subgroup 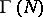 of level
of level 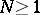 (
(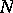 an integer) is the group of transformations
an integer) is the group of transformations 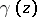 of the form (1) for which
of the form (1) for which 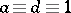 (
(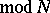 ),
), 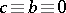 (
(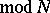 ). A subgroup
). A subgroup 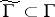 is called a congruence subgroup if
is called a congruence subgroup if 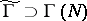 for some
for some 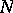 ; the least such
; the least such 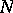 is called the level of
is called the level of 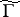 . Examples of congruence subgroups of level
. Examples of congruence subgroups of level 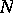 are: the group
are: the group 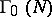 of transformations (1) with
of transformations (1) with  divisible by
divisible by 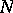 , and the group
, and the group 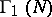 of transformations (1) with
of transformations (1) with 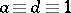 (
( ) and
) and 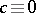 (
(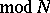 ). The index of
). The index of 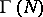 in the modular group is
in the modular group is 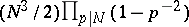 if
if 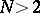 ,
, 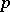 is a prime number, and 6 if
is a prime number, and 6 if 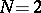 ; thus, each congruence subgroup has finite index in the modular group.
; thus, each congruence subgroup has finite index in the modular group.
Corresponding to each subgroup  of finite index in the modular group there is a complete algebraic curve
of finite index in the modular group there is a complete algebraic curve 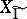 (a modular curve), obtained from the quotient space
(a modular curve), obtained from the quotient space 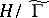 and the covering
and the covering 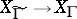 . The study of the branches of this covering allows one to find generators and relations for the congruence subgroup
. The study of the branches of this covering allows one to find generators and relations for the congruence subgroup 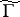 , the genus of
, the genus of 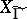 and to prove that there are subgroups of finite index in the modular group which are not congruence subgroups (see [3], [8], [7], Vol. 2). The study of presentations of the modular group was initiated in work (see [4], [6]) connected with the theory of modular forms. Such presentations were intensively studied within the theory of automorphic forms (see [7] and Automorphic form). Many results related to the modular group have been transferred to the case of arithmetic subgroups of algebraic Lie groups (cf. Arithmetic group; Lie algebra, algebraic).
and to prove that there are subgroups of finite index in the modular group which are not congruence subgroups (see [3], [8], [7], Vol. 2). The study of presentations of the modular group was initiated in work (see [4], [6]) connected with the theory of modular forms. Such presentations were intensively studied within the theory of automorphic forms (see [7] and Automorphic form). Many results related to the modular group have been transferred to the case of arithmetic subgroups of algebraic Lie groups (cf. Arithmetic group; Lie algebra, algebraic).
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) pp. Chapt.8 |
| [2] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) |
| [3] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971) |
| [4] | E. Hecke, "Analytische Arithmetik der positiven quadratischen Formen" , Mathematische Werke , Vandenhoeck & Ruprecht (1959) pp. 789–918 |
| [5] | F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , 1–2 , Teubner (1890–1892) |
| [6] | H.D. Kloosterman, "The behaviour of general theta functions under the modular group and the characters of binary modular congruence groups I, II" Ann. of Math. , 47 (1946) pp. 317–375; 376–417 |
| [7] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–6 , Lect. notes in math. , 320; 349; 350; 476; 601; 627 , Springer (1973–1977) |
| [8] | R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977) |
Modular group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_group&oldid=47871