Difference between revisions of "Modular curve"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47869 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A complete [[Algebraic curve|algebraic curve]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644101.png" /> uniformized by a subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644102.png" /> of finite index in the [[Modular group|modular group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644103.png" />; more precisely, a modular curve is a complete algebraic curve obtained from a quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644104.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644105.png" /> is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644106.png" /> of the rational points of the boundary of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644107.png" />). The best known examples of subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644108.png" /> of finite index in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m0644109.png" /> are the congruence subgroups containing a principal congruence subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441010.png" /> of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441011.png" /> for some integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441012.png" />, represented by the matrices |
| − | m0644101.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441013.png" /></td> </tr></table> | |
| − | |||
| − | + | (see [[Modular group|Modular group]]). The least such <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441014.png" /> is called the level of the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441015.png" />. In particular, the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441016.png" /> represented by matrices which are congruent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441017.png" /> to upper-triangular matrices has level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441018.png" />. Corresponding to each subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441019.png" /> of finite index there is a covering of the modular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441020.png" />, which ramifies only over the images of the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441023.png" />. For a congruence subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441024.png" /> the ramification of this covering allows one to determine the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441025.png" /> and to prove the existence of subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441026.png" /> of finite index in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441027.png" /> which are not congruence subgroups (see [[#References|[4]]], Vol. 2, [[#References|[2]]]). The genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441028.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441029.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441030.png" /> and equals | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | of the | ||
| − | |||
| − | of finite index in | ||
| − | are | ||
| − | of | ||
| − | for | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441031.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | (see [[ | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441032.png" /> a prime number, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441033.png" />. A modular curve is always defined over an algebraic number field (usually over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441034.png" /> or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [[#References|[2]]]). A holomorphic differential form on a modular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441035.png" /> is given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441036.png" /> by a differential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441037.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441038.png" /> is a holomorphic function) which is invariant under the transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441039.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441040.png" />; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441041.png" /> is a cusp form of weight 2 relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441042.png" />. The [[Zeta-function|zeta-function]] of a modular curve is a product of the Mellin transforms (cf. [[Mellin transform|Mellin transform]]) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [[#References|[7]]], [[#References|[8]]]). In particular, there is a hypothesis that each [[Elliptic curve|elliptic curve]] over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441043.png" /> (with conductor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441044.png" />) can be uniformized by modular functions of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441045.png" />. The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441046.png" />-adic zeta-function of a modular curve (see [[#References|[1]]]). |
| − | is | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | the | ||
| − | and | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A modular curve parametrizes a family of elliptic curves, being their moduli variety (see [[#References|[7]]], Vol. 2). In particular, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441047.png" /> a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441048.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441049.png" /> is in one-to-one correspondence with a pair consisting of an elliptic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441050.png" /> (analytically equivalent to a complex torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441051.png" />) and a point of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441052.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441053.png" /> (the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441054.png" />). | |
| − | |||
| − | + | Over each modular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441055.png" /> there is a natural algebraic fibre bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441056.png" /> of elliptic curves if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441057.png" /> does not contain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441058.png" />, compactified by degenerate curves above the parabolic points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441059.png" />. Powers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441060.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441061.png" /> is an integer, are called Kuga varieties (see [[#References|[3]]], [[#References|[5]]]). The zeta- functions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441062.png" /> are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [[#References|[3]]], [[#References|[7]]]). | |
| − | + | The rational points on a modular curve correspond to elliptic curves having rational points of finite order (or rational subgroups of points); their description (see [[#References|[6]]]) made it possible to solve the problem of determining the possible torsion subgroups of elliptic curves over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441063.png" />. | |
| − | ( | ||
| − | |||
| − | + | The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441064.png" /> with respect to decreasing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441065.png" />, which (in essence) coincides with the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441066.png" /> over the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441067.png" /> of rational adèles. On each modular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441068.png" /> this gives a non-trivial ring of correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441069.png" /> (a Hecke ring), which has applications in the theory of modular forms (cf. [[Modular form|Modular form]], [[#References|[3]]]). | |
| − | |||
| − | |||
| − | |||
| − | is | ||
| − | |||
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====References==== | |
| − | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" ''Math. USSR Izv.'' , '''6''' : 1 (1972) pp. 19–64 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''36''' : 1 (1972) pp. 19–66</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" ''Math. USSR Sb.'' , '''30''' : 1 (1976) pp. 119–142 ''Mat. Sb.'' , '''101''' : 1 (1976) pp. 131–157</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , '''1–2''' , Teubner (1890–1892)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" ''Ann. of Math.'' , '''82''' (1965) pp. 478–539</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441070.png" /> (d'après A. Ogg)" , ''Sem. Bourbaki 1974/1975'' , ''Lect. notes in math.'' , '''514''' , Springer (1976) pp. 238–255</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" ''Math. Ann.'' , '''168''' (1967) pp. 149–156</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====Comments==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985)</TD></TR></table> | ||
Revision as of 13:51, 7 June 2020
A complete algebraic curve  uniformized by a subgroup
uniformized by a subgroup  of finite index in the modular group
of finite index in the modular group  ; more precisely, a modular curve is a complete algebraic curve obtained from a quotient space
; more precisely, a modular curve is a complete algebraic curve obtained from a quotient space  , where
, where  is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to
is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to  of the rational points of the boundary of
of the rational points of the boundary of  ). The best known examples of subgroups
). The best known examples of subgroups  of finite index in
of finite index in  are the congruence subgroups containing a principal congruence subgroup
are the congruence subgroups containing a principal congruence subgroup  of level
of level 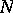 for some integer
for some integer 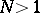 , represented by the matrices
, represented by the matrices
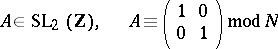 |
(see Modular group). The least such 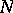 is called the level of the subgroup
is called the level of the subgroup  . In particular, the subgroup
. In particular, the subgroup  represented by matrices which are congruent
represented by matrices which are congruent  to upper-triangular matrices has level
to upper-triangular matrices has level  . Corresponding to each subgroup
. Corresponding to each subgroup 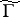 of finite index there is a covering of the modular curve
of finite index there is a covering of the modular curve 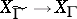 , which ramifies only over the images of the points
, which ramifies only over the images of the points 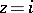 ,
,  ,
,  . For a congruence subgroup
. For a congruence subgroup 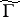 the ramification of this covering allows one to determine the genus of
the ramification of this covering allows one to determine the genus of  and to prove the existence of subgroups
and to prove the existence of subgroups 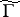 of finite index in
of finite index in  which are not congruence subgroups (see [4], Vol. 2, [2]). The genus of
which are not congruence subgroups (see [4], Vol. 2, [2]). The genus of 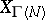 is
is  for
for  and equals
and equals
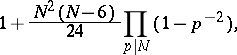 |
 a prime number, for
a prime number, for 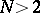 . A modular curve is always defined over an algebraic number field (usually over
. A modular curve is always defined over an algebraic number field (usually over 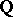 or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [2]). A holomorphic differential form on a modular curve
or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [2]). A holomorphic differential form on a modular curve 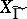 is given on
is given on  by a differential
by a differential 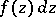 (where
(where 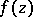 is a holomorphic function) which is invariant under the transformations
is a holomorphic function) which is invariant under the transformations 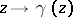 of
of  ; here
; here 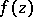 is a cusp form of weight 2 relative to
is a cusp form of weight 2 relative to 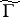 . The zeta-function of a modular curve is a product of the Mellin transforms (cf. Mellin transform) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [7], [8]). In particular, there is a hypothesis that each elliptic curve over
. The zeta-function of a modular curve is a product of the Mellin transforms (cf. Mellin transform) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [7], [8]). In particular, there is a hypothesis that each elliptic curve over  (with conductor
(with conductor 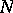 ) can be uniformized by modular functions of level
) can be uniformized by modular functions of level  . The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the
. The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the  -adic zeta-function of a modular curve (see [1]).
-adic zeta-function of a modular curve (see [1]).
A modular curve parametrizes a family of elliptic curves, being their moduli variety (see [7], Vol. 2). In particular, for 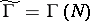 a point
a point  of
of 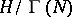 is in one-to-one correspondence with a pair consisting of an elliptic curve
is in one-to-one correspondence with a pair consisting of an elliptic curve  (analytically equivalent to a complex torus
(analytically equivalent to a complex torus 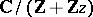 ) and a point of order
) and a point of order 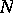 on
on  (the image of
(the image of  ).
).
Over each modular curve  there is a natural algebraic fibre bundle
there is a natural algebraic fibre bundle  of elliptic curves if
of elliptic curves if 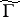 does not contain
does not contain 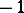 , compactified by degenerate curves above the parabolic points of
, compactified by degenerate curves above the parabolic points of 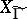 . Powers
. Powers  , where
, where 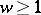 is an integer, are called Kuga varieties (see [3], [5]). The zeta- functions of
is an integer, are called Kuga varieties (see [3], [5]). The zeta- functions of  are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [3], [7]).
are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [3], [7]).
The rational points on a modular curve correspond to elliptic curves having rational points of finite order (or rational subgroups of points); their description (see [6]) made it possible to solve the problem of determining the possible torsion subgroups of elliptic curves over 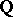 .
.
The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves  with respect to decreasing
with respect to decreasing 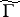 , which (in essence) coincides with the group
, which (in essence) coincides with the group 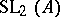 over the ring
over the ring 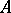 of rational adèles. On each modular curve
of rational adèles. On each modular curve  this gives a non-trivial ring of correspondences
this gives a non-trivial ring of correspondences 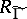 (a Hecke ring), which has applications in the theory of modular forms (cf. Modular form, [3]).
(a Hecke ring), which has applications in the theory of modular forms (cf. Modular form, [3]).
References
| [1] | Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" Math. USSR Izv. , 6 : 1 (1972) pp. 19–64 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 1 (1972) pp. 19–66 |
| [2] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971) |
| [3] | V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" Math. USSR Sb. , 30 : 1 (1976) pp. 119–142 Mat. Sb. , 101 : 1 (1976) pp. 131–157 |
| [4] | F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , 1–2 , Teubner (1890–1892) |
| [5] | M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" Ann. of Math. , 82 (1965) pp. 478–539 |
| [6] | B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires 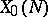 (d'après A. Ogg)" , Sem. Bourbaki 1974/1975 , Lect. notes in math. , 514 , Springer (1976) pp. 238–255 (d'après A. Ogg)" , Sem. Bourbaki 1974/1975 , Lect. notes in math. , 514 , Springer (1976) pp. 238–255 |
| [7] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–6 , Lect. notes in math. , 320; 349; 350; 476; 601; 627 , Springer (1973–1977) |
| [8] | A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" Math. Ann. , 168 (1967) pp. 149–156 |
Comments
References
| [a1] | N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985) |
Modular curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_curve&oldid=47869