Model theory of the real exponential function
A branch of model theory studying the elementary theory 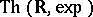 of the ordered field
of the ordered field 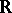 of real numbers with the real exponential function
of real numbers with the real exponential function 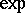 (cf. Exponential function, real). It is motivated by Tarski's question [a7], p. 45, whether
(cf. Exponential function, real). It is motivated by Tarski's question [a7], p. 45, whether 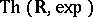 is decidable.
is decidable.
A. Wilkie showed in [a8] that 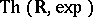 is model complete. Combining this with Khovanskii's finiteness theorem [a5], it follows that this theory is
is model complete. Combining this with Khovanskii's finiteness theorem [a5], it follows that this theory is  -minimal. In fact, Wilkie first studies expansions (cf. Structure) of
-minimal. In fact, Wilkie first studies expansions (cf. Structure) of 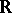 by a Pfaffian chain of functions (see also [a2]): Fix
by a Pfaffian chain of functions (see also [a2]): Fix 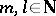 and an open set
and an open set 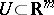 containing the closed unit box
containing the closed unit box 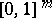 . A Pfaffian chain of functions on
. A Pfaffian chain of functions on  is a sequence
is a sequence 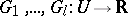 of analytic functions (cf. Analytic function) for which there exist polynomials
of analytic functions (cf. Analytic function) for which there exist polynomials 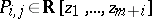 (for
(for 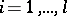 ;
; 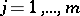 ) such that
) such that
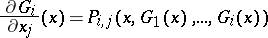 |
for all  . Wilkie shows that the expansion of
. Wilkie shows that the expansion of 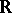 by a Pfaffian chain of functions restricted to the closed unit box has a model-complete theory. In particular, the expansion
by a Pfaffian chain of functions restricted to the closed unit box has a model-complete theory. In particular, the expansion 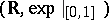 of
of 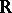 by the restricted exponential function has a model-complete theory. Wilkie then deduces the model completeness of
by the restricted exponential function has a model-complete theory. Wilkie then deduces the model completeness of 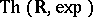 from this last result. An alternative proof of the model completeness, and an axiomatization of
from this last result. An alternative proof of the model completeness, and an axiomatization of 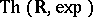 over
over 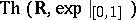 , was found by J.P. Ressayre in 1991 (see [a3] for a generalization of Ressayre's result).
, was found by J.P. Ressayre in 1991 (see [a3] for a generalization of Ressayre's result).
In [a6], A. Macintyre and Wilkie show that 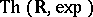 is decidable provided that the real version of Schanuel's conjecture (cf. Algebraic independence) is true.
is decidable provided that the real version of Schanuel's conjecture (cf. Algebraic independence) is true.
The theory 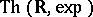 does not admit elimination of quantifiers. In fact, an expansion of
does not admit elimination of quantifiers. In fact, an expansion of 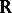 by a family of total real-analytic functions (see [a1]) admits elimination of quantifiers if and only if each function is semi-algebraic, i.e., has a semi-algebraic graph (cf. Semi-algebraic set). However, let
by a family of total real-analytic functions (see [a1]) admits elimination of quantifiers if and only if each function is semi-algebraic, i.e., has a semi-algebraic graph (cf. Semi-algebraic set). However, let 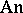 denote the family of restricted real-analytic functions, i.e., functions
denote the family of restricted real-analytic functions, i.e., functions 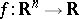 , for all
, for all 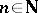 , which are given on
, which are given on 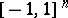 by a power series converging on a neighbourhood of
by a power series converging on a neighbourhood of 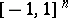 and are set equal to
and are set equal to  outside of
outside of 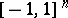 . It is shown in [a3] that the expansion
. It is shown in [a3] that the expansion 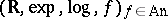 admits elimination of quantifiers. The authors also give a complete axiomatization of
admits elimination of quantifiers. The authors also give a complete axiomatization of 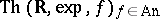 , and establish that it is
, and establish that it is  -minimal. In [a4] they construct a model of this theory which is not Archimedean and use it to solve a problem raised by G.H. Hardy: they show that the compositional inverse of the function
-minimal. In [a4] they construct a model of this theory which is not Archimedean and use it to solve a problem raised by G.H. Hardy: they show that the compositional inverse of the function 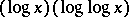 is not asymptotic at
is not asymptotic at 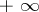 to a composition of semi-algebraic functions,
to a composition of semi-algebraic functions, 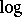 and
and 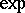 .
.
References
| [a1] | L. van den Dries, "Remarks on Tarski's problem concerning $({\bf R},+,\cdot,\exp)$" G. Lolli (ed.) G. Longo (ed.) A. Marcja (ed.) , Logic Colloquium '82 , North-Holland (1984) pp. 97–121 |
| [a2] | L. van den Dries, "Tarski's problem and Pfaffian functions" J.B. Paris (ed.) A.J. Wilkie (ed.) G.M. Wilmers (ed.) , Logic Colloquium '84 , North-Holland (1986) pp. 59–90 |
| [a3] | L. van den Dries, A.J. Macintyre, D. Marker, "The elementary theory of restricted analytic fields with exponentiation" Ann. of Math. , 140 (1994) pp. 183–205 |
| [a4] | L. van den Dries, A.J. Macintyre, D. Marker, "Logarithmic-exponential power series" J. London Math. Soc. 56 (1997) 417-434. Zbl 0924.12007 |
| [a5] | A. Khovanskii, "On a class of systems of transcendental equations" Soviet Math. Dokl. , 22 (1980) pp. 762–765 (In Russian) |
| [a6] | A.J. Macintyre, A.J. Wilkie, "On the decidability of the real exponential field" P.G. Odifreddi (ed.) , Kreisel 70th Birthday Volume , CLSI (1995) |
| [a7] | A. Tarski, J.C.C. McKinsey, "A decision method for elementary algebra and geometry" , Univ. California Press (1951) |
| [a8] | A.J. Wilkie, "Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function" J. Amer. Math. Soc. , 9 : 4 (1996) |
Model theory of the real exponential function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Model_theory_of_the_real_exponential_function&oldid=13098