Model for calculations
computational model
A typical problem used as a model for investigating and developing numerical methods for some class of problems. For example, in the theory of quadrature the problem of calculating integrals of functions satisfying a condition 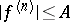 is considered. The processing of methods for the solution of the Cauchy problem for systems of ordinary differential equations historically was done by investigating the properties of the methods on models from a sequence of increasing complexity (with integration interval
is considered. The processing of methods for the solution of the Cauchy problem for systems of ordinary differential equations historically was done by investigating the properties of the methods on models from a sequence of increasing complexity (with integration interval 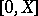 ):
):
1) the equation 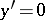 ;
;
2) the equation  ,
, 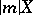 of order 1 (models 1) and 2) correspond to the problem of integration on small time intervals of systems with smooth solutions);
of order 1 (models 1) and 2) correspond to the problem of integration on small time intervals of systems with smooth solutions);
3a) the equation  ,
, 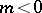 ,
, 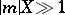 ; this model corresponds to the problem of integration on large time intervals of systems with stable solutions;
; this model corresponds to the problem of integration on large time intervals of systems with stable solutions;
3b) the equation 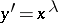 ; a model of an equation with singularities in the derivatives of solutions;
; a model of an equation with singularities in the derivatives of solutions;
4) the system 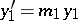 ,
, 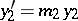 ,
, 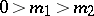 ,
, 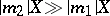 ,
, 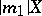 of order 1; a model of so-called stiff differential systems (cf. Stiff differential system), in which one component varies relatively slowly and the other rapidly.
of order 1; a model of so-called stiff differential systems (cf. Stiff differential system), in which one component varies relatively slowly and the other rapidly.
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Model for calculations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Model_for_calculations&oldid=14160