Mixing
A property of a dynamical system (a cascade 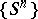 or a flow (continuous-time dynamical system)
or a flow (continuous-time dynamical system)  ) having a finite invariant measure
) having a finite invariant measure 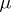 , in which for any two measurable subsets
, in which for any two measurable subsets 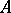 and
and 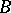 of the phase space
of the phase space 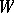 , the measure
, the measure
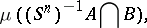 |
or, respectively,
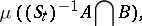 |
tends to
 |
as 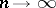 , or, respectively, as
, or, respectively, as 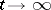 . If the transformations
. If the transformations 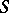 and
and 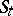 are invertible, then in the definition of mixing one may replace the pre-images of the original set
are invertible, then in the definition of mixing one may replace the pre-images of the original set 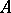 with respect to these transformations by the direct images
with respect to these transformations by the direct images  and
and 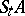 , which are easier to visualize. If a system has the mixing property, one also says that the system is mixing, while in the case of a mixing cascade
, which are easier to visualize. If a system has the mixing property, one also says that the system is mixing, while in the case of a mixing cascade 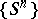 , one says that the endomorphism
, one says that the endomorphism 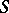 generating it in the measure space
generating it in the measure space  also is mixing (has the property of mixing).
also is mixing (has the property of mixing).
In ergodic theory, properties related to mixing are considered: multiple mixing and weak mixing (see [1]; in the old literature the latter is often called mixing in the wide sense or simply mixing, while mixing was called mixing in the strong sense). A property intermediate between mixing and weak mixing has also been discussed [2]. All these properties are stronger than ergodicity.
There is an analogue of mixing for systems having an infinite invariant measure [3].
References
| [1] | P.R. Halmos, "Lectures on ergodic theory" , Math. Soc. Japan (1956) |
| [2] | H. Furstenberg, B. Weiss, "The finite multipliers of infinite ergodic transformations" N.G. Markley (ed.) J.C. Martin (ed.) W. Perrizo (ed.) , The Structure of Attractors in Dynamical Systems , Lect. notes in math. , 668 , Springer (1978) pp. 127–132 |
| [3] | U. Krengel, L. Sucheston, "On mixing in infinite measure spaces" Z. Wahrscheinlichkeitstheor. Verw. Geb. , 13 : 2 (1969) pp. 150–164 |
Comments
For a cascade 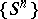 on a finite measure space
on a finite measure space 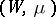 the notion of weak mixing as defined above is equivalent to the property that the cascade generated by
the notion of weak mixing as defined above is equivalent to the property that the cascade generated by 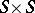 on the measure space
on the measure space 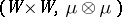 , where
, where 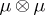 denotes the product measure, is ergodic (cf. Ergodicity; Metric transitivity). See [1].
denotes the product measure, is ergodic (cf. Ergodicity; Metric transitivity). See [1].
For topological dynamical systems the notions of strong and weak mixing have been defined as well [a2]. A flow on a topological space 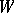 is said to be topologically weakly mixing whenever the flow
is said to be topologically weakly mixing whenever the flow  on
on 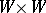 (with the usual product topology) is topologically ergodic; equivalently: whenever for every choice of four non-empty open subsets
(with the usual product topology) is topologically ergodic; equivalently: whenever for every choice of four non-empty open subsets 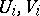 (
(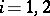 ) of
) of 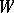 where exists a
where exists a 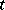 such that
such that 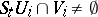 for
for 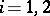 . On compact spaces the weakly mixing minimal flows are the minimal flows that have no non-trivial equicontinuous factors; see [a1], p. 133. A flow
. On compact spaces the weakly mixing minimal flows are the minimal flows that have no non-trivial equicontinuous factors; see [a1], p. 133. A flow 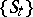 on a space
on a space 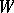 is said to be topologically strongly mixing whenever for every two non-empty open subsets
is said to be topologically strongly mixing whenever for every two non-empty open subsets 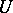 and
and 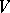 of
of 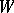 there exists a value
there exists a value 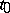 such that
such that 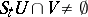 for all
for all  . For example, the geodesic flow on a complete two-dimensional Riemannian manifold of constant negative curvature is topologically strongly mixing; see [a3], 13.49. For cascades, the definitions are analogous.
. For example, the geodesic flow on a complete two-dimensional Riemannian manifold of constant negative curvature is topologically strongly mixing; see [a3], 13.49. For cascades, the definitions are analogous.
References
| [a1] | J. Auslander, "Minimal flows and their extensions" , North-Holland (1988) |
| [a2] | H. Furstenberg, "Disjointness in ergodic theory, minimal sets and a problem in diophantine approximations" Math. Systems Th. , 1 (1967) pp. 1–49 |
| [a3] | W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) |
Mixing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mixing&oldid=11708