Mittag-Leffler theorem

The Mittag-Leffler theorem on expansion of a meromorphic function (see , ) is one of the basic theorems in analytic function theory, giving for meromorphic functions an analogue of the expansion of a rational function into the simplest partial fractions. Let 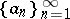be a sequence of distinct complex numbers,

and let be a sequence of rational functions of the form

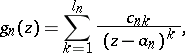(1)

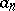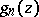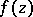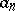so that is the unique pole of the corresponding function . Then there are meromorphic functions in the complex -plane having poles at , and only there, with given principal parts (1) of the Laurent series corresponding to the points . All these functions 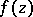are representable in the form of a Mittag-Leffler expansion

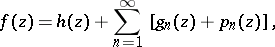(2)

where 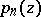is a polynomial chosen in dependence of 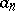and 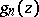so that the series (2) is uniformly convergent (after the removal of a finite number of terms) on any compact set 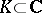and 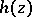is an arbitrary entire function.

The Mittag-Leffler theorem implies that any given meromorphic functio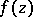n in 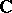with poles 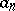and corresponding principal parts 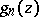of the Laurent expansion of 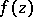in a neighbourhood of 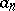can be expanded in a series (2) where the entire function 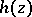is determined by 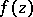. G. Mittag-Leffler gave a general construction of the polynomials 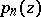; finding the entire function 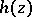relative to a given 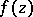is sometimes a more difficult problem. To obtain (2) it is possible to apply methods of the theory of residues (cf. Residue of an analytic function, see also –).

A generalization of the quoted theorem, also due to Mittag-Leffler, states that for any domain 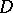of the extended complex plane 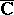, any sequence 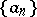of points 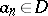all limit points of which are in the boundary 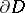, and corresponding principal parts (1), there is a function 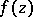, meromorphic in 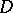, having poles at 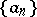, and only there, with the given principal parts (1). In this form the Mittag-Leffler theorem generalizes to open Riemann surfaces 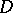(see ); for the existence of meromorphic functions on compact Riemann surfaces with given singularities see Abelian differential; Differential on a Riemann surface; Riemann–Roch theorem. The Mittag-Leffler theorem is also true for abstract meromorphic functions 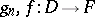, , 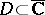with values in a Banach space 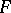(see ).

Another generalization of the Mittag-Leffler theorem states that for any sequence 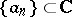, , 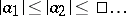, 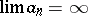and corresponding functions

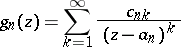that are entire functions of the variable 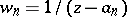, there is a single-valued analytic function 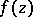having singular points at 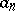, and only there, and with principal parts 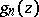(see ).

For analytic functions of several complex variables a generalization of the Mittag-Leffler problem on the construction of a function with given singularities is the first (additive) Cousin problem (cf. Cousin problems). In this connection the following equivalent statement of the Mittag-Leffler theorem is often useful. Let 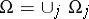, where the 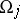are open sets in 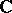, and let there be given meromorphic functions 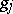, respectively, on the sets 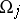, where the differences are regular functions on the intersections 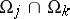for all 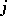and 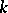. Then there is on a meromorphic function 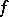such that the differences 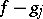are regular on 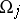for all 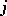(see , ).

For the Mittag-Leffler theorem on the expansion of single-valued branches of an analytic function in a star see Star of a function element.

References

[1]	G. Mittag-Leffler, "En metod att analytisk framställa en funktion at rationel karacte..." Öfversigt Kongl. Vetenskap-Akad. Förhandlinger , 33 (1876) pp. 3–16
[2]	G. Mittag-Leffler, "Sur la répresentation analytique des fonctions monogènes uniformes d'une variable indépendante" Acta Math. , 4 (1884) pp. 1–79
[3]	E. Goursat, "Cours d'analyse mathématique" , Gauthier-Villars (1927)
[4]	A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian)
[5]	B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian)
[6]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973)
[7]	H. Behnke, F. Sommer, "Theorie der analytischen Funktionen einer komplexen Veränderlichen" , Springer (1972)
[8]	L. Schwartz, "Analyse mathématique" , 2 , Hermann (1967)

References

[a1]	J.B. Conway, "Functions of one complex variable" , Springer (1978)
[a2]	M. Heins, "Complex function theory" , Acad. Press (1968)