Mittag-Leffler function
From Encyclopedia of Mathematics
An entire function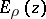 
of a complex variable 
, introduced by G. Mittag-Leffler [1] as a generalization of the exponential function:
 |
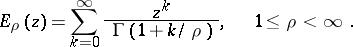Since the Mittag-Leffler function and the more general functions of Mittag-Leffler type
 |
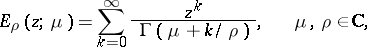are widely used in integral representations and transforms of analytic functions, their properties, in particular asymptotic properties, have been studied in great detail (see [2], [3]).
References
| [1] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène" Acta Math. , 29 (1905) pp. 101–181 |
| [2] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
| [3] | A.A. Gol'dberg, I.V. Ostrovskii, "Value distribution of meromorphic functions" , Moscow (1970) (In Russian) |
Comments
References
| [a1] | M.L. Cartwright, "Integral functions" , Cambridge Univ. Press (1962) |
How to Cite This Entry:
Mittag-Leffler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mittag-Leffler_function&oldid=16180
Mittag-Leffler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mittag-Leffler_function&oldid=16180
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article