Minkowski space
A four-dimensional pseudo-Euclidean space of signature 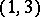 , suggested by H. Minkowski (1908) as a geometric model of space-time in the special theory of relativity (see ). Corresponding to each event there is a point of Minkowski space, three coordinates of which represent its coordinates in the three-dimensional space; the fourth coordinate is
, suggested by H. Minkowski (1908) as a geometric model of space-time in the special theory of relativity (see ). Corresponding to each event there is a point of Minkowski space, three coordinates of which represent its coordinates in the three-dimensional space; the fourth coordinate is 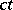 , where
, where  is the velocity of light and
is the velocity of light and 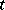 is the time of the event. The space-time relationship between two events is characterized by the so-called square interval:
is the time of the event. The space-time relationship between two events is characterized by the so-called square interval:
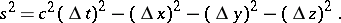 |
The interval in Minkowski space plays a role similar to that of distance in Euclidean geometry. A vector with positive square interval is called a time-like vector, one with negative square interval, a space-like vector, one with square interval zero, a null or isotropic vector. A curve with a time-like tangent vector at each point is called a time-like curve. Space-like and isotropic curves are similarly defined. An event at a given moment of time is called a world point; a set of world points describing the development of some process or phenomenon through time is called a world line. If a vector joining neighbouring world points is time-like, then there is a frame of reference in which the events project to one and the same point of three-dimensional space. The time separating the events in this frame of reference is equal to 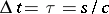 , where
, where  is the so-called proper time. There is no frame of reference in which these events can be simultaneous (that is, have the same time coordinate
is the so-called proper time. There is no frame of reference in which these events can be simultaneous (that is, have the same time coordinate 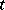 ). If the vector joining the world points of two events is space-like, then there is a frame of reference in which these two events occur simultaneously; they are not connected by a causal relation; the modulus of the square interval defines the spatial distance between the points (events) in this frame of reference. A tangent vector to a world line is a time-like vector. The tangent vector to a light ray is an isotropic vector.
). If the vector joining the world points of two events is space-like, then there is a frame of reference in which these two events occur simultaneously; they are not connected by a causal relation; the modulus of the square interval defines the spatial distance between the points (events) in this frame of reference. A tangent vector to a world line is a time-like vector. The tangent vector to a light ray is an isotropic vector.
The motions of Minkowski space, that is, the interval-preserving transformations, are the Lorentz transformations (cf. Lorentz transformation).
A generalization of Minkowski space is the pseudo-Riemannian space used in the construction of the theory of gravitation.
References
| [1a] | H. Minkowski, "Raum und Zeit" Phys. Z. Sowjetunion , 10 (1909) pp. 104- ((Reprint in: Lorentz–Einstein–Minkowski, Teubner, 1922)) |
| [1b] | H. Minkowski, "Das Relativitätsprinzip" Jahresber. Deutsch. Math. Verein , 24 (1915) pp. 372- |
| [2] | L.D. Landau, E.M. Lifshitz, "The classical theory of fields" , Addison-Wesley (1962) (Translated from Russian) |
| [3] | V.A. [V.A. Fok] Fock, "The theory of space, time and gravitation" , Macmillan (1954) (Translated from Russian) |
| [4] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [5] | J.L. Synge, "Relativity: the general theory" , North-Holland (1960) |
Comments
See in particular [a3], pp. 10-11 and Chapt. 3, and [a4]–[a6] for material on the pseudo-Riemannian spaces used in gravitational theories.
References
| [a1] | M. Dillard-Bleik, "Analysis, manifolds and physics" , North-Holland (1977) (Translated from French) |
| [a2] | S. Weinberg, "Gravitation and cosmology" , Wiley (1972) pp. Chapt. 3 |
| [a3] | A.L. Besse, "Einstein manifolds" , Springer (1987) |
| [a4] | S.W. Hawking, G.F.R. Ellis, "The large scale structure of space-time" , Cambridge Univ. Press (1973) |
| [a5] | C.W. Misner, K.S. Thorne, J.A. Wheeler, "Gravitation" , Freeman (1973) |
| [a6] | B. O'Neill, "Semi-Riemannian geometry (with applications to relativity)" , Acad. Press (1983) |
Minkowski space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minkowski_space&oldid=14606