Minkowski addition
The Minkowski sum of two sets  ,
,  in
in  -dimensional Euclidean space
-dimensional Euclidean space  is defined as the set
is defined as the set
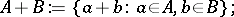 |
one also defines  for real
for real  . Coupled with the notion of volume, this Minkowski addition leads to the Brunn–Minkowski theorem and is the basis for the Brunn–Minkowski theory of convex bodies (i.e., compact convex sets).
. Coupled with the notion of volume, this Minkowski addition leads to the Brunn–Minkowski theorem and is the basis for the Brunn–Minkowski theory of convex bodies (i.e., compact convex sets).
Repeated Minkowski addition of compact sets has a convexifying effect; this is made precise by the Shapley–Folkman–Starr theorem.
The structure of Minkowski addition is well studied on the space  of convex bodies in
of convex bodies in  .
. 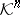 with Minkowski addition and multiplication by non-negative scalars is a convex cone. The mapping
with Minkowski addition and multiplication by non-negative scalars is a convex cone. The mapping 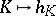 , where
, where
 |
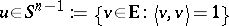 |
(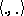 being the scalar product) is the support function, maps this cone isomorphically into the space
being the scalar product) is the support function, maps this cone isomorphically into the space 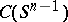 of continuous real functions on
of continuous real functions on  . The image is precisely the closed convex cone of restrictions of sublinear functions. (For corresponding results in topological vector spaces, see [a2] and its bibliography.)
. The image is precisely the closed convex cone of restrictions of sublinear functions. (For corresponding results in topological vector spaces, see [a2] and its bibliography.)
For convex bodies 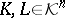 , the body
, the body  is called a summand of
is called a summand of 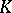 if there exists an
if there exists an  such that
such that 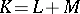 . Each summand of
. Each summand of 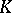 is a non-empty intersection of a family of translates of
is a non-empty intersection of a family of translates of 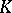 ; the converse is true for
; the converse is true for  .
. 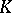 is called indecomposable if every summand of K is of the form
is called indecomposable if every summand of K is of the form 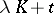 with
with  and
and 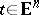 . In the plane
. In the plane  , the indecomposable convex bodies are precisely the segments and the triangles. For
, the indecomposable convex bodies are precisely the segments and the triangles. For 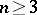 , every simplicial convex polytope in
, every simplicial convex polytope in 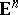 is indecomposable, hence most convex bodies (in the Baire category sense, cf. also Baire set) are indecomposable.
is indecomposable, hence most convex bodies (in the Baire category sense, cf. also Baire set) are indecomposable.
A mapping  from
from 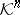 into an Abelian group is called Minkowski additive if
into an Abelian group is called Minkowski additive if 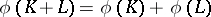 for all
for all  . Such mappings are special valuations and play a particular role in the investigation of valuations on convex bodies. Common examples are the mean width and the Steiner point
. Such mappings are special valuations and play a particular role in the investigation of valuations on convex bodies. Common examples are the mean width and the Steiner point  . A surjective mapping
. A surjective mapping 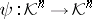 with
with  that commutes with rigid motions and is continuous with respect to the Hausdorff metric is trivial, namely of the form
that commutes with rigid motions and is continuous with respect to the Hausdorff metric is trivial, namely of the form 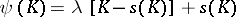 with
with  .
.
References
| [a1] | R. Schneider, "Convex bodies: the Brunn–Minkowski theory" , Cambridge Univ. Press (1993) |
| [a2] | R. Urbanski, "A generalization of the Minkowski–Rådström–Hörmander theorem" Bull. Acad. Polon. Sci. Ser. Sci. Math., Astr., Phys. , 24 (1976) pp. 709 – 715 |
Minkowski addition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minkowski_addition&oldid=16121