Difference between revisions of "Minimal set"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | A minimal set in a Riemannian space is a generalization of a [[Minimal surface|minimal surface]]. A minimal set is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638901.png" />-dimensional closed subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638902.png" /> in a Riemannian space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638903.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638904.png" />, such that for some subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638905.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638906.png" />-dimensional [[Hausdorff measure|Hausdorff measure]] zero the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638907.png" /> is a differentiable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638908.png" />-dimensional minimal surface (that is, is an extremum of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638909.png" />-dimensional volume functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389010.png" />, defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389011.png" />-dimensional surfaces imbedded in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389012.png" />). The notion of a | + | A minimal set in a Riemannian space is a generalization of a [[Minimal surface|minimal surface]]. A minimal set is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638901.png" />-dimensional closed subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638902.png" /> in a Riemannian space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638903.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638904.png" />, such that for some subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638905.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638906.png" />-dimensional [[Hausdorff measure|Hausdorff measure]] zero the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638907.png" /> is a differentiable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638908.png" />-dimensional minimal surface (that is, is an extremum of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m0638909.png" />-dimensional volume functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389010.png" />, defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389011.png" />-dimensional surfaces imbedded in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389012.png" />). The notion of a "minimal set" amalgamates several mathematical ideas called upon to serve in the so-called multi-dimensional [[Plateau problem|Plateau problem]] (cf. also [[Plateau problem, multi-dimensional|Plateau problem, multi-dimensional]]). |
''A.T. Fomenko'' | ''A.T. Fomenko'' | ||
| − | A minimal set in a topological dynamical system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389013.png" /> is a non-empty closed invariant (that is, consisting wholly of trajectories) subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389014.png" /> of the phase space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389015.png" /> of the system which does not have proper closed invariant subsets. The latter is equivalent to saying that each trajectory in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389016.png" /> is everywhere dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389017.png" />. The notion of a minimal set was introduced by G.D. Birkhoff (see [[#References|[1]]]) for the case of a flow (the | + | A minimal set in a topological dynamical system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389013.png" /> is a non-empty closed invariant (that is, consisting wholly of trajectories) subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389014.png" /> of the phase space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389015.png" /> of the system which does not have proper closed invariant subsets. The latter is equivalent to saying that each trajectory in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389016.png" /> is everywhere dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389017.png" />. The notion of a minimal set was introduced by G.D. Birkhoff (see [[#References|[1]]]) for the case of a flow (the "time" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389018.png" /> running through the real numbers). He proved (see [[#References|[1]]], [[#References|[2]]]) that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389019.png" /> is a compact minimal set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389020.png" />, then for any neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389022.png" /> the set of those <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389023.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389024.png" /> is relatively dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389025.png" /> (that is, there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389026.png" /> such that in each "time interval" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389027.png" /> of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389028.png" /> there is at least one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389029.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389030.png" />); conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389031.png" /> is a complete metric space and a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389032.png" /> has the above property, then the closure of its trajectory <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389033.png" /> is a compact minimal set (the same is true for a [[Cascade|cascade]]; regarding more general groups of transformations see, for example, [[#References|[3]]] and [[#References|[4]]]). Birkhoff called this property of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389034.png" /> (and its trajectory) recurrence; another terminology, suggested by W.H. Gottschalk and G.A. Hedlund [[#References|[3]]], is also used, in which this property is called almost-periodicity of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389035.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389036.png" />, then the dynamical system itself is called minimal. |
If a trajectory has compact closure, then it contains a minimal set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389037.png" /> (for semi-groups of continuous transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389038.png" />, with non-negative real or integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389039.png" />, an analogue of this result holds, where in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389040.png" /> the transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389041.png" /> are even invertible [[#References|[5]]]). However, research into the limit behaviour of the trajectories of a dynamical system does not reduce to the study of only the minimal sets of the latter. A minimal set of a smooth flow of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389042.png" /> on a two-dimensional closed surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389043.png" /> has a very simple structure: it is either a point, a closed trajectory or the whole surface, which is then a torus (Schwarz's theorem, [[#References|[6]]]). In the general case the structure of a minimal set can be very complicated (in this connection, in addition to what is said in [[#References|[2]]]–[[#References|[4]]] it must be said that minimality of a dynamical system places no restrictions on its ergodic properties with respect to any of its invariant measures, [[#References|[7]]]). Minimal sets are the fundamental objects of study in [[Topological dynamics|topological dynamics]]. | If a trajectory has compact closure, then it contains a minimal set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389037.png" /> (for semi-groups of continuous transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389038.png" />, with non-negative real or integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389039.png" />, an analogue of this result holds, where in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389040.png" /> the transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389041.png" /> are even invertible [[#References|[5]]]). However, research into the limit behaviour of the trajectories of a dynamical system does not reduce to the study of only the minimal sets of the latter. A minimal set of a smooth flow of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389042.png" /> on a two-dimensional closed surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389043.png" /> has a very simple structure: it is either a point, a closed trajectory or the whole surface, which is then a torus (Schwarz's theorem, [[#References|[6]]]). In the general case the structure of a minimal set can be very complicated (in this connection, in addition to what is said in [[#References|[2]]]–[[#References|[4]]] it must be said that minimality of a dynamical system places no restrictions on its ergodic properties with respect to any of its invariant measures, [[#References|[7]]]). Minimal sets are the fundamental objects of study in [[Topological dynamics|topological dynamics]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) {{MR|1555257}} {{ZBL|53.0733.03}} {{ZBL|53.0732.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) {{MR|0121520}} {{ZBL|0089.29502}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) {{MR|0074810}} {{ZBL|0067.15204}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.U. Bronshtein, "Extensions of minimal transformation groups" , Sijthoff & Noordhoff (1979) (Translated from Russian) {{MR|0550605}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian) {{MR|0690064}} {{ZBL|0499.43005}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> P. Hartman, "Ordinary differential equations" , Wiley (1964) {{MR|0171038}} {{ZBL|0125.32102}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" ''J. Soviet Math.'' , '''7''' (1977) pp. 974–1065 ''Itogi. Nauk. i Tekhn. Mat. Anal.'' , '''13''' (1975) pp. 129–262 {{MR|0584389}} {{ZBL|0399.28011}} </TD></TR></table> |
''D.V. Anosov'' | ''D.V. Anosov'' | ||
====Comments==== | ====Comments==== | ||
| − | The terminology around the notions of recurrence and almost periodicity of points in a topological dynamical system is confusing. These are two mainstreams of nomenclature, represented by [[#References|[1]]], [[#References|[2]]], [[#References|[a8]]] on the one hand, and by [[#References|[3]]], [[#References|[a1]]], [[#References|[a2]]] on the other. The type of point mentioned above, namely, a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389044.png" /> such that for every neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389045.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389046.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389047.png" /> is relatively dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389048.png" />, is called almost periodic in [[#References|[3]]], [[#References|[4]]], [[#References|[a1]]], [[#References|[a2]]], and almost recurrent in [[#References|[2]]] and [[#References|[a8]]]. (In [[#References|[2]]], [[#References|[a8]]], almost periodicity has another meaning.) Formally, the notion of a recurrent point as defined in [[#References|[1]]], [[#References|[2]]], [[#References|[a8]]] is different: see [[Recurrent point|Recurrent point]]; a recurrent point is always [[#References|[3]]]-almost periodic (i.e., almost-recurrent), but not conversely. In a dynamical system on a complete metric space the two notions coincide. (In [[#References|[3]]] the notion of a recurrent point is used in the meaning of | + | The terminology around the notions of recurrence and almost periodicity of points in a topological dynamical system is confusing. These are two mainstreams of nomenclature, represented by [[#References|[1]]], [[#References|[2]]], [[#References|[a8]]] on the one hand, and by [[#References|[3]]], [[#References|[a1]]], [[#References|[a2]]] on the other. The type of point mentioned above, namely, a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389044.png" /> such that for every neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389045.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389046.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389047.png" /> is relatively dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389048.png" />, is called almost periodic in [[#References|[3]]], [[#References|[4]]], [[#References|[a1]]], [[#References|[a2]]], and almost recurrent in [[#References|[2]]] and [[#References|[a8]]]. (In [[#References|[2]]], [[#References|[a8]]], almost periodicity has another meaning.) Formally, the notion of a recurrent point as defined in [[#References|[1]]], [[#References|[2]]], [[#References|[a8]]] is different: see [[Recurrent point|Recurrent point]]; a recurrent point is always [[#References|[3]]]-almost periodic (i.e., almost-recurrent), but not conversely. In a dynamical system on a complete metric space the two notions coincide. (In [[#References|[3]]] the notion of a recurrent point is used in the meaning of "positively and negatively Poisson stable" .) What Birkhoff proved was the equivalence of recurrence of a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389049.png" /> (according to the terminology of [[#References|[1]]], [[#References|[2]]]) and the property that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389050.png" /> has a compact minimal orbit closure, provided the phase space is a complete metric space. Using the terminology of [[#References|[3]]] one can show: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389051.png" /> has a compact minimal orbit closure, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389052.png" /> is an almost-periodic point (no conditions on the phase space); conversely, an almost-periodic point has a minimal orbit closure, which is compact if the phase space is locally compact and Hausdorff (no metrizability assumed). |
The classification of compact minimal sets in topological dynamics is a largely unsolved problem. Only for special classes something can be said (cf. [[Distal dynamical system|Distal dynamical system]]); see [[#References|[4]]], [[#References|[a2]]] and [[#References|[a1]]]. Unsolved is also the problem as to which (compact) Hausdorff spaces can be the phase space of a minimal flow or a minimal cascade. In this respect, Schwarz's theorem, mentioned above, gives a partial solution for compact surfaces; for a generalization, see [[#References|[a4]]]. A Klein bottle cannot be minimal under a continuous flow (the [[Kneser theorem|Kneser theorem]], see also [[#References|[a6]]]), neither can the real projective plane (see [[#References|[a5]]]). Still open is Gottschalk's conjecture (a particular case of Seifert's conjecture): <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389053.png" /> cannot be the phase space of a minimal flow; see Appendix II of [[#References|[a7]]] for references (the Seifert conjecture states that any smooth flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389054.png" /> has a periodic orbit; there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389055.png" />-counterexample, [[#References|[a9]]]). For results about cascades, see [[#References|[a3]]], [[#References|[a10]]]. | The classification of compact minimal sets in topological dynamics is a largely unsolved problem. Only for special classes something can be said (cf. [[Distal dynamical system|Distal dynamical system]]); see [[#References|[4]]], [[#References|[a2]]] and [[#References|[a1]]]. Unsolved is also the problem as to which (compact) Hausdorff spaces can be the phase space of a minimal flow or a minimal cascade. In this respect, Schwarz's theorem, mentioned above, gives a partial solution for compact surfaces; for a generalization, see [[#References|[a4]]]. A Klein bottle cannot be minimal under a continuous flow (the [[Kneser theorem|Kneser theorem]], see also [[#References|[a6]]]), neither can the real projective plane (see [[#References|[a5]]]). Still open is Gottschalk's conjecture (a particular case of Seifert's conjecture): <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389053.png" /> cannot be the phase space of a minimal flow; see Appendix II of [[#References|[a7]]] for references (the Seifert conjecture states that any smooth flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389054.png" /> has a periodic orbit; there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m063/m063890/m06389055.png" />-counterexample, [[#References|[a9]]]). For results about cascades, see [[#References|[a3]]], [[#References|[a10]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Auslander, "Minimal flows and their extensions" , North-Holland (1988) {{MR|0956049}} {{ZBL|0654.54027}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Ellis, "Lectures on topological dynamics" , Benjamin (1969) {{MR|0267561}} {{ZBL|0193.51502}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. Glasner, B. Weiss, "On the construction of minimal skew products" ''Israel J. Math.'' , '''34''' (1979) pp. 321–336 {{MR|0570889}} {{ZBL|0434.54032}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Gutierrez, "Smoothing continuous flows on two-manifolds and recurrences" ''Ergod. Th. Dynam. Sys.'' , '''6''' (1986) pp. 17–44 {{MR|0837974}} {{ZBL|0606.58042}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P.-F. Lam, "Inverses of recurrent and periodic points under homomorphisms of dynamical systems" ''Math. Systems Theory'' , '''6''' (1972) pp. 26–36 {{MR|0301718}} {{ZBL|0229.54035}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> N.G. Markley, "The Poincaré–Bendixson theorem for the Klein bottle" ''Trans. Amer. Math. Soc.'' , '''135''' (1969) pp. 159–165 {{MR|234442}} {{ZBL|0175.50101}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Markus, "Lectures in differentiable dynamics" , Amer. Math. Soc. (1980) pp. Appendix II {{MR|0309152}} {{ZBL|0214.50701}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> K.S. Sibirskii, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian) {{MR|0357987}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> P.A. Schweitzer, "Counterexamples to the Seifert conjecture and opening closed leaves of foliations" ''Amer. of Math. (2)'' , '''100''' (1974) pp. 386–400 {{MR|0356086}} {{ZBL|0295.57010}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> A. Fahti, M. Herman, "Existence de diffeomorphismes minimaux" ''Astérisque'' , '''49''' (1977) pp. 37–59 {{MR|482843}} {{ZBL|}} </TD></TR></table> |
Revision as of 16:59, 15 April 2012
A minimal set in a Riemannian space is a generalization of a minimal surface. A minimal set is a 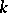 -dimensional closed subset
-dimensional closed subset 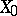 in a Riemannian space
in a Riemannian space 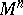 ,
, 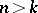 , such that for some subset
, such that for some subset 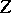 of
of 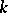 -dimensional Hausdorff measure zero the set
-dimensional Hausdorff measure zero the set 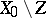 is a differentiable
is a differentiable 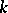 -dimensional minimal surface (that is, is an extremum of the
-dimensional minimal surface (that is, is an extremum of the 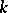 -dimensional volume functional
-dimensional volume functional 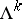 , defined on
, defined on 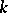 -dimensional surfaces imbedded in
-dimensional surfaces imbedded in 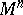 ). The notion of a "minimal set" amalgamates several mathematical ideas called upon to serve in the so-called multi-dimensional Plateau problem (cf. also Plateau problem, multi-dimensional).
). The notion of a "minimal set" amalgamates several mathematical ideas called upon to serve in the so-called multi-dimensional Plateau problem (cf. also Plateau problem, multi-dimensional).
A.T. Fomenko
A minimal set in a topological dynamical system 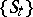 is a non-empty closed invariant (that is, consisting wholly of trajectories) subset
is a non-empty closed invariant (that is, consisting wholly of trajectories) subset 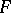 of the phase space
of the phase space 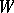 of the system which does not have proper closed invariant subsets. The latter is equivalent to saying that each trajectory in
of the system which does not have proper closed invariant subsets. The latter is equivalent to saying that each trajectory in 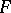 is everywhere dense in
is everywhere dense in 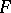 . The notion of a minimal set was introduced by G.D. Birkhoff (see [1]) for the case of a flow (the "time"
. The notion of a minimal set was introduced by G.D. Birkhoff (see [1]) for the case of a flow (the "time" 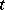 running through the real numbers). He proved (see [1], [2]) that if
running through the real numbers). He proved (see [1], [2]) that if  is a compact minimal set and
is a compact minimal set and 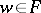 , then for any neighbourhood
, then for any neighbourhood 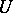 of
of 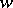 the set of those
the set of those 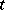 for which
for which 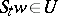 is relatively dense in
is relatively dense in 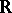 (that is, there is an
(that is, there is an 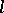 such that in each "time interval"
such that in each "time interval" 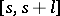 of length
of length 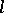 there is at least one
there is at least one 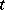 with
with  ); conversely, if
); conversely, if 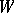 is a complete metric space and a point
is a complete metric space and a point 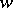 has the above property, then the closure of its trajectory
has the above property, then the closure of its trajectory 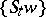 is a compact minimal set (the same is true for a cascade; regarding more general groups of transformations see, for example, [3] and [4]). Birkhoff called this property of
is a compact minimal set (the same is true for a cascade; regarding more general groups of transformations see, for example, [3] and [4]). Birkhoff called this property of  (and its trajectory) recurrence; another terminology, suggested by W.H. Gottschalk and G.A. Hedlund [3], is also used, in which this property is called almost-periodicity of the point
(and its trajectory) recurrence; another terminology, suggested by W.H. Gottschalk and G.A. Hedlund [3], is also used, in which this property is called almost-periodicity of the point 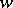 . If
. If  , then the dynamical system itself is called minimal.
, then the dynamical system itself is called minimal.
If a trajectory has compact closure, then it contains a minimal set 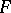 (for semi-groups of continuous transformations
(for semi-groups of continuous transformations 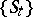 , with non-negative real or integer
, with non-negative real or integer 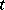 , an analogue of this result holds, where in
, an analogue of this result holds, where in 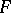 the transformations
the transformations 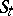 are even invertible [5]). However, research into the limit behaviour of the trajectories of a dynamical system does not reduce to the study of only the minimal sets of the latter. A minimal set of a smooth flow of class
are even invertible [5]). However, research into the limit behaviour of the trajectories of a dynamical system does not reduce to the study of only the minimal sets of the latter. A minimal set of a smooth flow of class 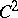 on a two-dimensional closed surface
on a two-dimensional closed surface 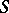 has a very simple structure: it is either a point, a closed trajectory or the whole surface, which is then a torus (Schwarz's theorem, [6]). In the general case the structure of a minimal set can be very complicated (in this connection, in addition to what is said in [2]–[4] it must be said that minimality of a dynamical system places no restrictions on its ergodic properties with respect to any of its invariant measures, [7]). Minimal sets are the fundamental objects of study in topological dynamics.
has a very simple structure: it is either a point, a closed trajectory or the whole surface, which is then a torus (Schwarz's theorem, [6]). In the general case the structure of a minimal set can be very complicated (in this connection, in addition to what is said in [2]–[4] it must be said that minimality of a dynamical system places no restrictions on its ergodic properties with respect to any of its invariant measures, [7]). Minimal sets are the fundamental objects of study in topological dynamics.
References
| [1] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) MR1555257 Zbl 53.0733.03 Zbl 53.0732.01 |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) MR0121520 Zbl 0089.29502 |
| [3] | W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) MR0074810 Zbl 0067.15204 |
| [4] | I.U. Bronshtein, "Extensions of minimal transformation groups" , Sijthoff & Noordhoff (1979) (Translated from Russian) MR0550605 |
| [5] | B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian) MR0690064 Zbl 0499.43005 |
| [6] | P. Hartman, "Ordinary differential equations" , Wiley (1964) MR0171038 Zbl 0125.32102 |
| [7] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 (1977) pp. 974–1065 Itogi. Nauk. i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 MR0584389 Zbl 0399.28011 |
D.V. Anosov
Comments
The terminology around the notions of recurrence and almost periodicity of points in a topological dynamical system is confusing. These are two mainstreams of nomenclature, represented by [1], [2], [a8] on the one hand, and by [3], [a1], [a2] on the other. The type of point mentioned above, namely, a point 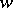 such that for every neighbourhood
such that for every neighbourhood 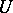 of
of 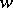 the set
the set 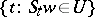 is relatively dense in
is relatively dense in  , is called almost periodic in [3], [4], [a1], [a2], and almost recurrent in [2] and [a8]. (In [2], [a8], almost periodicity has another meaning.) Formally, the notion of a recurrent point as defined in [1], [2], [a8] is different: see Recurrent point; a recurrent point is always [3]-almost periodic (i.e., almost-recurrent), but not conversely. In a dynamical system on a complete metric space the two notions coincide. (In [3] the notion of a recurrent point is used in the meaning of "positively and negatively Poisson stable" .) What Birkhoff proved was the equivalence of recurrence of a point
, is called almost periodic in [3], [4], [a1], [a2], and almost recurrent in [2] and [a8]. (In [2], [a8], almost periodicity has another meaning.) Formally, the notion of a recurrent point as defined in [1], [2], [a8] is different: see Recurrent point; a recurrent point is always [3]-almost periodic (i.e., almost-recurrent), but not conversely. In a dynamical system on a complete metric space the two notions coincide. (In [3] the notion of a recurrent point is used in the meaning of "positively and negatively Poisson stable" .) What Birkhoff proved was the equivalence of recurrence of a point 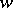 (according to the terminology of [1], [2]) and the property that
(according to the terminology of [1], [2]) and the property that  has a compact minimal orbit closure, provided the phase space is a complete metric space. Using the terminology of [3] one can show: If
has a compact minimal orbit closure, provided the phase space is a complete metric space. Using the terminology of [3] one can show: If 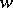 has a compact minimal orbit closure, the
has a compact minimal orbit closure, the 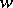 is an almost-periodic point (no conditions on the phase space); conversely, an almost-periodic point has a minimal orbit closure, which is compact if the phase space is locally compact and Hausdorff (no metrizability assumed).
is an almost-periodic point (no conditions on the phase space); conversely, an almost-periodic point has a minimal orbit closure, which is compact if the phase space is locally compact and Hausdorff (no metrizability assumed).
The classification of compact minimal sets in topological dynamics is a largely unsolved problem. Only for special classes something can be said (cf. Distal dynamical system); see [4], [a2] and [a1]. Unsolved is also the problem as to which (compact) Hausdorff spaces can be the phase space of a minimal flow or a minimal cascade. In this respect, Schwarz's theorem, mentioned above, gives a partial solution for compact surfaces; for a generalization, see [a4]. A Klein bottle cannot be minimal under a continuous flow (the Kneser theorem, see also [a6]), neither can the real projective plane (see [a5]). Still open is Gottschalk's conjecture (a particular case of Seifert's conjecture): 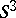 cannot be the phase space of a minimal flow; see Appendix II of [a7] for references (the Seifert conjecture states that any smooth flow on
cannot be the phase space of a minimal flow; see Appendix II of [a7] for references (the Seifert conjecture states that any smooth flow on 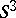 has a periodic orbit; there is a
has a periodic orbit; there is a 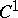 -counterexample, [a9]). For results about cascades, see [a3], [a10].
-counterexample, [a9]). For results about cascades, see [a3], [a10].
References
| [a1] | J. Auslander, "Minimal flows and their extensions" , North-Holland (1988) MR0956049 Zbl 0654.54027 |
| [a2] | R. Ellis, "Lectures on topological dynamics" , Benjamin (1969) MR0267561 Zbl 0193.51502 |
| [a3] | G. Glasner, B. Weiss, "On the construction of minimal skew products" Israel J. Math. , 34 (1979) pp. 321–336 MR0570889 Zbl 0434.54032 |
| [a4] | C. Gutierrez, "Smoothing continuous flows on two-manifolds and recurrences" Ergod. Th. Dynam. Sys. , 6 (1986) pp. 17–44 MR0837974 Zbl 0606.58042 |
| [a5] | P.-F. Lam, "Inverses of recurrent and periodic points under homomorphisms of dynamical systems" Math. Systems Theory , 6 (1972) pp. 26–36 MR0301718 Zbl 0229.54035 |
| [a6] | N.G. Markley, "The Poincaré–Bendixson theorem for the Klein bottle" Trans. Amer. Math. Soc. , 135 (1969) pp. 159–165 MR234442 Zbl 0175.50101 |
| [a7] | L. Markus, "Lectures in differentiable dynamics" , Amer. Math. Soc. (1980) pp. Appendix II MR0309152 Zbl 0214.50701 |
| [a8] | K.S. Sibirskii, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian) MR0357987 |
| [a9] | P.A. Schweitzer, "Counterexamples to the Seifert conjecture and opening closed leaves of foliations" Amer. of Math. (2) , 100 (1974) pp. 386–400 MR0356086 Zbl 0295.57010 |
| [a10] | A. Fahti, M. Herman, "Existence de diffeomorphismes minimaux" Astérisque , 49 (1977) pp. 37–59 MR482843 |
Minimal set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_set&oldid=13164