Milnor sphere
A smooth manifold homeomorphic (and piecewise-linearly isomorphic), but not diffeomorphic, to the sphere 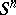 . The first example of such a manifold was constructed by J. Milnor in 1956 (see [1]); the same example was the first example of homeomorphic but not diffeomorphic manifolds.
. The first example of such a manifold was constructed by J. Milnor in 1956 (see [1]); the same example was the first example of homeomorphic but not diffeomorphic manifolds.
Construction of a Milnor sphere.
Any compact smooth oriented closed manifold, homotopically equivalent to 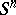 ,
, 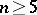 , is homeomorphic (and even piecewise-linearly isomorphic) to
, is homeomorphic (and even piecewise-linearly isomorphic) to 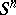 (see Poincaré conjecture, generalized;
(see Poincaré conjecture, generalized; 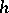 -cobordism). The index of a closed smooth almost parallelizable manifold of dimension
-cobordism). The index of a closed smooth almost parallelizable manifold of dimension 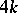 is divisible by a number
is divisible by a number  which exponentially increases with
which exponentially increases with 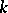 . For any
. For any 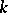 there is a parallelizable manifold
there is a parallelizable manifold 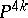 of index 8 (namely, the plumbing construction of Milnor) whose boundary
of index 8 (namely, the plumbing construction of Milnor) whose boundary  is, for
is, for  , a homotopy sphere (see [2], [6]). If
, a homotopy sphere (see [2], [6]). If  were diffeomorphic to the sphere
were diffeomorphic to the sphere  , then the manifold
, then the manifold  obtained from
obtained from 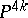 by the addition of a cone over the boundary would be a smooth almost parallelizable closed manifold of index 8. Thus
by the addition of a cone over the boundary would be a smooth almost parallelizable closed manifold of index 8. Thus 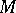 is a Milnor sphere.
is a Milnor sphere.
There are other examples of Milnor spheres (see [5]).
Classification of Milnor spheres.
In the sequel the term "Milnor sphere" will be used also for the standard sphere 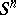 . There are 28 distinct (non-diffeomorphic)
. There are 28 distinct (non-diffeomorphic) 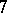 -dimensional Milnor spheres.
-dimensional Milnor spheres.
The set of all smooth structures on the piecewise-linear sphere is equivalent to the set of elements of the group  . The latter group is trivial for
. The latter group is trivial for 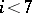 , so in the
, so in the 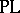 -case any Milnor sphere of dimension less than 7 is diffeomorphic to the standard sphere.
-case any Milnor sphere of dimension less than 7 is diffeomorphic to the standard sphere.
Let  be the set of classes of
be the set of classes of 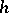 -cobordant
-cobordant  -dimensional smooth manifolds which are homotopically equivalent to
-dimensional smooth manifolds which are homotopically equivalent to 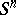 . The operation of connected sum transforms this set into a group, where the zero is the
. The operation of connected sum transforms this set into a group, where the zero is the 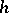 -cobordism class of
-cobordism class of 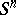 . For
. For 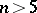 the elements of
the elements of  are in one-to-one correspondence with the diffeomorphism classes of
are in one-to-one correspondence with the diffeomorphism classes of  -dimensional Milnor spheres. To calculate the groups
-dimensional Milnor spheres. To calculate the groups 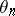 ,
, 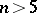 , one specifies (see [3]) a trivialization of the stable normal bundle (a framing) of the Milnor sphere
, one specifies (see [3]) a trivialization of the stable normal bundle (a framing) of the Milnor sphere 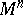 . This is possible since
. This is possible since 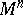 is stably parallelizable. The framed manifold obtained defines an element of the stable homotopy group
is stably parallelizable. The framed manifold obtained defines an element of the stable homotopy group 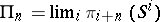 . This element depends, in general, on the choice of the framing (
. This element depends, in general, on the choice of the framing ( is a "multi-valued mapping" ). Let
is a "multi-valued mapping" ). Let  be the subgroup in
be the subgroup in 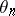 consisting of Milnor spheres that bound parallelizable manifolds. This multi-valued mapping induces a homomorphism
consisting of Milnor spheres that bound parallelizable manifolds. This multi-valued mapping induces a homomorphism  , where
, where 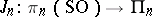 is the stationary Whitehead homomorphism and
is the stationary Whitehead homomorphism and 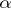 is an isomorphism. The calculation of the group
is an isomorphism. The calculation of the group  reduces to the problem of calculating
reduces to the problem of calculating  and
and 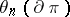 (unsolved, 1989), which is done by means of surgery (cf. Morse surgery) of the manifold (preserving the boundary). Let
(unsolved, 1989), which is done by means of surgery (cf. Morse surgery) of the manifold (preserving the boundary). Let 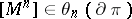 , that is,
, that is,  and
and  is parallelizable. If
is parallelizable. If 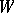 is a contractible manifold, then after cutting out from
is a contractible manifold, then after cutting out from 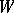 a small disc, the manifold
a small disc, the manifold  is
is 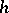 -cobordant to
-cobordant to 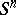 , that is,
, that is,  . If
. If  is even, then it is possible to modify
is even, then it is possible to modify 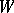 by means of surgery so that the new manifold
by means of surgery so that the new manifold 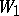 with
with 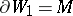 is contractible (here one requires parallelizability of
is contractible (here one requires parallelizability of 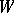 and
and 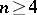 ). Thus
). Thus 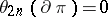 .
.
The case  . If the index
. If the index 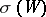 of
of 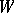 is
is  , then
, then 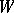 can be transformed by surgery into a contractible manifold, so that in this case
can be transformed by surgery into a contractible manifold, so that in this case 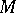 is a standard sphere. If
is a standard sphere. If  and
and 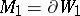 , then
, then  and
and 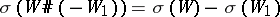 (here
(here  is the connected sum or the boundary connected sum of two manifolds
is the connected sum or the boundary connected sum of two manifolds  and
and 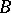 ). If
). If 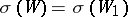 , then
, then  , so that the invariant
, so that the invariant  defines an element
defines an element  . If
. If  and
and 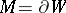 , then
, then 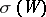 is divisible by
is divisible by 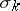 . Conversely, for any
. Conversely, for any  there is a smooth closed manifold
there is a smooth closed manifold 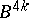 with
with 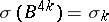 ; therefore, if
; therefore, if 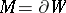 and
and 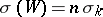 , then
, then 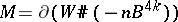 , where
, where 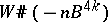 is parallelizable and
is parallelizable and  . The element
. The element 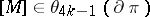 is completely determined by the residue of
is completely determined by the residue of 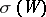 modulo
modulo 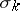 , and different residues determine different manifolds. Since
, and different residues determine different manifolds. Since  takes any value divisible by
takes any value divisible by  ,
,  . E.g.,
. E.g., 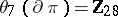 , and
, and 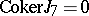 , so
, so 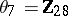 .
.
The case 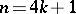 . Let
. Let  . If the Kervaire invariant of
. If the Kervaire invariant of 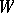 is zero, that is,
is zero, that is,  , then
, then 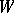 can be converted by surgery into a contractible manifold, that is,
can be converted by surgery into a contractible manifold, that is,  . Now let
. Now let  . Since for
. Since for  there is no smooth closed almost-parallelizable (which in dimension
there is no smooth closed almost-parallelizable (which in dimension 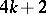 is equivalent to stably-parallelizable) manifold with Kervaire invariant not equal to zero,
is equivalent to stably-parallelizable) manifold with Kervaire invariant not equal to zero, 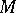 is not diffeomorphic to
is not diffeomorphic to 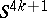 . In this case
. In this case  , that is,
, that is, 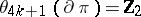 . For
. For 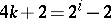 and those
and those  for which there is a manifold with non-zero Kervaire invariant,
for which there is a manifold with non-zero Kervaire invariant, 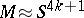 , that is,
, that is, 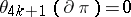 , but the question of describing all such
, but the question of describing all such 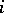 has not been solved (1989). However, for
has not been solved (1989). However, for 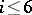 the answer is positive. Thus
the answer is positive. Thus 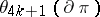 is
is 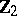 or
or  .
.
There is another representation of a Milnor sphere. Let 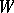 be an algebraic variety in
be an algebraic variety in  with equation
with equation
 |
and let 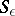 be the
be the 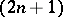 -dimensional sphere of (small) radius
-dimensional sphere of (small) radius  with centre at the origin. For suitable values of
with centre at the origin. For suitable values of 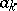 ,
,  is a Milnor sphere (see [4]). For example, for
is a Milnor sphere (see [4]). For example, for  and
and 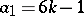 ,
, 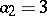 ,
,  and
and  , all 28
, all 28  -dimensional Milnor spheres are obtained.
-dimensional Milnor spheres are obtained.
References
| [1] | J.W. Milnor, "On manifolds homeomorphic to the 7-sphere" Ann. of Math. , 64 (1956) pp. 399–405 |
| [2] | J.W. Milnor, "Bernoulli numbers, homotopy groups, and a theorem of Rohlin" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 454–458 |
| [3] | M.A. Kervaire, J.W. Milnor, "Groups of homotopy spheres" Ann. of Math. , 77 (1963) pp. 504–537 |
| [4] | J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) |
| [5] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
| [6] | W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) |
Comments
The general problem of constructing different smooth structures on a topological manifold has received much attention since the above article was written (around 1982). In particular, it has been proven that  has different smooth structures (but not
has different smooth structures (but not 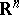 for
for  ). A general reference is [a1].
). A general reference is [a1].
References
| [a1] | D.S. Freed, K.K. Uhlenbeck, "Instantons and four-manifolds" , Springer (1984) |
Milnor sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Milnor_sphere&oldid=12635