Mikhailov criterion
All roots of a polynomial
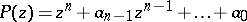 |
with real coefficients have strictly negative real part if and only if the complex-valued function 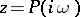 of a real variable
of a real variable 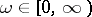 describes a curve (the Mikhailov hodograph) in the complex
describes a curve (the Mikhailov hodograph) in the complex  -plane which starts on the positive real semi-axis, does not hit the origin and successively generates an anti-clockwise motion through
-plane which starts on the positive real semi-axis, does not hit the origin and successively generates an anti-clockwise motion through  quadrants. (An equivalent condition is: The radius vector
quadrants. (An equivalent condition is: The radius vector 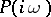 , as
, as 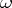 increases from
increases from  to
to  , never vanishes and monotonically rotates in a positive direction through an angle
, never vanishes and monotonically rotates in a positive direction through an angle 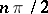 .)
.)
This criterion was first suggested by A.V. Mikhailov [1]. It is equivalent to the Routh–Hurwitz criterion; however, it is geometric in character and does not require the verification of determinant inequalities (see [2], [3]). The Mikhailov criterion gives a necessary and sufficient condition for the asymptotic stability of a linear differential equation of order  ,
,
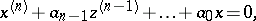 |
with constant coefficients, or of a linear system
 |
with a constant matrix 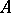 , the characteristic polynomial of which is
, the characteristic polynomial of which is 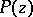 (see [4]).
(see [4]).
Mikhailov's criterion is one of the frequency criteria for the stability of linear systems of automatic control (closely related to, for example, the Nyquist criterion). A generalization of Mikhailov's criterion is known for systems of automatic control with delay, for impulse systems (see [5]), and there is also an analogue of Mikhailov's criterion for non-linear control systems (see [6]).
References
| [1] | A.V. Mikhailov, Avtomat. i Telemekh. , 3 (1938) pp. 27–81 |
| [2] | N.G. Chebotarev, N.N. Meiman, "The Routh–Hurwitz problem for polynomials and entire functions" Trudy Mat. Inst. Steklov. , 76 (1949) (In Russian) |
| [3] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [4] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [5] | L.S. Gnoenskii, G.A. Kamenskii, L.E. El'sgol'ts, "Mathematical foundations of the theory of control systems" , Moscow (1969) (In Russian) |
| [6] | A. Blaquiére, "Mécanique non-lineaire" , Gauthier-Villars (1960) |
Comments
Recently a generalization of stability criteria with respect to roots of polynomials has been found. It is named after V.L. Kharitonov [a1]. The generalization is that the coefficients 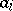 in the polynomial
in the polynomial 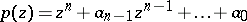 take values in given intervals
take values in given intervals 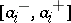 ,
,  . The problem addressed by Kharitonov is whether all polynomials
. The problem addressed by Kharitonov is whether all polynomials 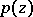 with
with 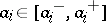 are strictly stable. It turns out that the stability of only four specific polynomials has to be investigated in order to answer this question.
are strictly stable. It turns out that the stability of only four specific polynomials has to be investigated in order to answer this question.
References
| [a1] | V.L. Kharitonov, "Asymptotic stability of an equilibrium position of a family of systems of linear differential equations" Differential Eq. , 14 : 11 (1978) pp. 1483–1485 Differentsial'nye Uravnen. , 14 : 11 (1978) pp. 2086–2088 |
| [a2] | B.R. Barmish, "New tools for robustness analysis" , IEEE Proc. 27th Conf. Decision and Control, Austin, Texas, December 1988 , IEEE (1988) pp. 1–6 |
| [a3] | S. LaSalle, "Stability by Liapunov's direct method" , Acad. Press (1961) |
Mikhailov criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mikhailov_criterion&oldid=12540