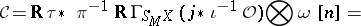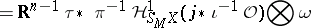Microlocal analysis considers (generalized, hyper-) functions, operators, etc. in the "microlocal" range. Here, "microlocal" means seeing the matter more locally than usual by introducing the (cotangential) direction at every point. In Fourier analysis it corresponds to viewing things locally in both  and
and  . In view of the uncertainty principle, this is possible only by considering the objects modulo regular parts. This idea was first used in the study of pseudo-differential operators by P.D. Lax, S. Mizohata, L. Hörmander, etc. V.P. Maslov has enriched the theory by the introduction of a canonical structure. M. Sato has constructed the sheaf of micro-functions on the cotangent sphere bundle
. In view of the uncertainty principle, this is possible only by considering the objects modulo regular parts. This idea was first used in the study of pseudo-differential operators by P.D. Lax, S. Mizohata, L. Hörmander, etc. V.P. Maslov has enriched the theory by the introduction of a canonical structure. M. Sato has constructed the sheaf of micro-functions on the cotangent sphere bundle  of the base space
of the base space  as the basic object of microlocal analysis.
as the basic object of microlocal analysis.
Micro-analyticity of hyperfunctions.
A hyperfunction  is said to be micro-analytic at
is said to be micro-analytic at  if on a neighbourhood of
if on a neighbourhood of  it admits analytic continuation into the half-space
it admits analytic continuation into the half-space  , in the sense that it admits a boundary-value representation
, in the sense that it admits a boundary-value representation  such that
such that 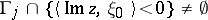 for every
for every 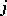 . This is equivalent to saying that near
. This is equivalent to saying that near 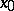 ,
,  , where
, where 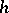 is the germ of a real-analytic function and
is the germ of a real-analytic function and 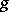 is a Fourier hyperfunction (cf. Hyperfunction) exponentially decreasing in a conic neighbourhood of
is a Fourier hyperfunction (cf. Hyperfunction) exponentially decreasing in a conic neighbourhood of 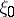 . The set of points
. The set of points  at which
at which 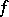 is not micro-analytic is called the singular spectrum of
is not micro-analytic is called the singular spectrum of 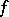 , and is denoted by
, and is denoted by 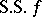 . By definition,
. By definition,
where 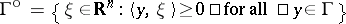 is the dual cone of
is the dual cone of 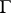 . Conversely, a hyperfunction satisfying this estimate can be written in the form
. Conversely, a hyperfunction satisfying this estimate can be written in the form 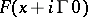 .
.
Operations and the singular spectrum.
The following inclusions hold:
Here, the operations are legitimate if the vector  does not appear in the
does not appear in the 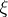 -component of the right-hand side. In particular, under coordinate transformation the singular spectrum behaves like a subset of
-component of the right-hand side. In particular, under coordinate transformation the singular spectrum behaves like a subset of  . Restriction
. Restriction  is possible if
is possible if 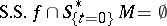 , in which case
, in which case  is said to contain
is said to contain 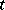 as real-analytic parameter at
as real-analytic parameter at 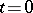 , and then
, and then
where 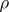 denotes projection on the
denotes projection on the 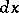 components. The dual assertion is:
components. The dual assertion is:
The combination of these assertions gives a convolution, dual to the product:
Let 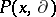 be a linear differential operator with real-analytic coefficients and let
be a linear differential operator with real-analytic coefficients and let 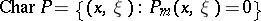 be its characteristic manifold. Then
be its characteristic manifold. Then
(Sato's fundamental theorem). Hence Cauchy data for solutions can be specified on a non-characteristic manifold. Holmgren's uniqueness theorem holds with these data. More generally, for any hyperfunction  ,
,  implies
implies 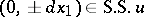 (the Kashiwara–Kawai Holmgren-type theorem); further, the fibre
(the Kashiwara–Kawai Holmgren-type theorem); further, the fibre  of
of 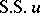 at
at  has the form
has the form  , where
, where 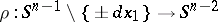 denotes projection to the equator
denotes projection to the equator 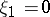 (the watermelon theorem).
(the watermelon theorem).
Decomposition of singular spectra.
One has
where the twisted phase 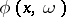 is a real-analytic function of
is a real-analytic function of 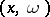 which is of positive type in
which is of positive type in  (that is,
(that is, 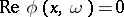 implies
implies 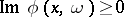 ), is homogeneous of degree 1 in
), is homogeneous of degree 1 in 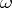 , and
, and 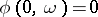 ,
, 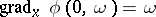 ; and the vector
; and the vector  is such that
is such that  . This is a generalization of the classical Radon decomposition, in which
. This is a generalization of the classical Radon decomposition, in which
The component, regarded as a hyperfunction of  , has a singular spectrum with only one direction
, has a singular spectrum with only one direction 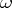 . Via convolution it gives a similar decomposition of general hyperfunctions. If
. Via convolution it gives a similar decomposition of general hyperfunctions. If  also satisfies
also satisfies 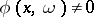 for
for 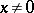 , then the singular spectrum of the component as a hyperfunction of
, then the singular spectrum of the component as a hyperfunction of  is precisely one point
is precisely one point 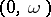 ; this is useful in applications. Typical examples are:
; this is useful in applications. Typical examples are:
(Kashiwara example);
(Bony example). For such a decomposition 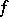 is micro-analytic at
is micro-analytic at 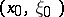 if and only if
if and only if 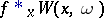 is real analytic in
is real analytic in 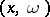 at
at 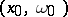 .
.
The Fourier–Bros–Iagolnitzer transform of a hyperfunction 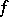 (the FBI-transform of
(the FBI-transform of 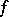 ) is
) is
where 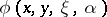 is a real-analytic function satisfying: 1) for
is a real-analytic function satisfying: 1) for 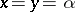 one has
one has 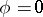 and
and 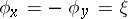 ; and 2)
; and 2)  for some
for some  . A typical example of such a
. A typical example of such a 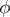 is
is
A hyperfunction  is micro-analytic at
is micro-analytic at 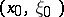 if and only if for some (equivalently, any) modification of
if and only if for some (equivalently, any) modification of  with compact support its FBI-transform is exponentially decreasing with respect to
with compact support its FBI-transform is exponentially decreasing with respect to  uniformly in
uniformly in 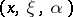 in a neighbourhood of
in a neighbourhood of 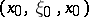 . Integration of the inversion formula over the radial variable gives the formula
. Integration of the inversion formula over the radial variable gives the formula
This supplies a partition of unity of the sheaf 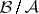 . All these arguments are compatible with the corresponding theory of (analytic) wave front sets for distributions.
. All these arguments are compatible with the corresponding theory of (analytic) wave front sets for distributions.
The sheaf 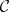 of micro-functions on
of micro-functions on 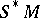 is the sheaf associated with the pre-sheaf
is the sheaf associated with the pre-sheaf
The sequence of sheaves on 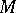 :
:
is exact. Here  denotes projection. By definition,
denotes projection. By definition, 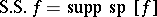 for a hyperfunction
for a hyperfunction 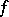 . The sheaf
. The sheaf  is flabby, which implies the possibility of arbitrary modification of hyperfunctions preserving the singular spectrum. Analytic pseudo-differential operators (cf. Pseudo-differential operator) and micro-differential operators naturally act on
is flabby, which implies the possibility of arbitrary modification of hyperfunctions preserving the singular spectrum. Analytic pseudo-differential operators (cf. Pseudo-differential operator) and micro-differential operators naturally act on 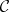 as sheaf homomorphisms. They act isomorphically at a non-characteristic point. Canonical transforms induce ring isomorphisms of the sheaf of pseudo-differential operators. Using these, a simple characteristic system of pseudo-differential equations can be locally reduced to the direct sum of copies of de Rham, Cauchy–Riemann and Lewy–Mizohata equations (the fundamental structure theorem).
as sheaf homomorphisms. They act isomorphically at a non-characteristic point. Canonical transforms induce ring isomorphisms of the sheaf of pseudo-differential operators. Using these, a simple characteristic system of pseudo-differential equations can be locally reduced to the direct sum of copies of de Rham, Cauchy–Riemann and Lewy–Mizohata equations (the fundamental structure theorem).
The sheaf  is constructed from the sheaf
is constructed from the sheaf 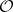 by Sato micro-localization: Let
by Sato micro-localization: Let 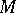 be a real-analytic manifold and
be a real-analytic manifold and 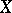 a complex neighbourhood of it. Let
a complex neighbourhood of it. Let 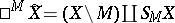 be the real blowing-up,
be the real blowing-up, 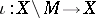 ,
, 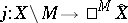 the canonical inclusions, and let
the canonical inclusions, and let 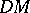 be the subset of the fibre product of
be the subset of the fibre product of 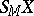 and
and 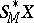 over
over 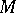 defined by
defined by  ; let
; let 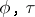 be the canonical projections to the factors. Let
be the canonical projections to the factors. Let  be the orientation sheaf of
be the orientation sheaf of  . Then
. Then
(the fundamental vanishing theorem). This argument can be generalized to the second micro-localization of micro-functions with respect to a holomorphic parameter or to micro-localization of any sheaf.
For additional references see also Hyperfunction.
References
| [a1] | M. Kashiwara, "Microfunctions and pseudo-differential equations" H. Komatsu (ed.) , Hyperfunctions and Pseudo-differential Equations, Part II , Lect. notes in math. , 287 , Springer (1973) pp. 263–529 |
| [a2] | M. Kashiwara, "Systems of micro-differential equations" , Birkhäuser (1983) (Translated from French) |
| [a3] | J. Sjöstrand, "Singularités analytiques microlocales" Astérisque , 95 (1982) |
| [a4] | Y. Laurent, "Théorie de la deuxième microlocalisation dans le domaine complexe" , Birkhäuser (1985) |
| [a5] | M. Kashiwara, P. Schapira, "Microlocal study of sheaves" Astérisque , 128 (1986) |
 and
and  . In view of the uncertainty principle, this is possible only by considering the objects modulo regular parts. This idea was first used in the study of pseudo-differential operators by P.D. Lax, S. Mizohata, L. Hörmander, etc. V.P. Maslov has enriched the theory by the introduction of a canonical structure. M. Sato has constructed the sheaf of micro-functions on the cotangent sphere bundle
. In view of the uncertainty principle, this is possible only by considering the objects modulo regular parts. This idea was first used in the study of pseudo-differential operators by P.D. Lax, S. Mizohata, L. Hörmander, etc. V.P. Maslov has enriched the theory by the introduction of a canonical structure. M. Sato has constructed the sheaf of micro-functions on the cotangent sphere bundle  of the base space
of the base space  as the basic object of microlocal analysis.
as the basic object of microlocal analysis.
 is said to be micro-analytic at
is said to be micro-analytic at  if on a neighbourhood of
if on a neighbourhood of  it admits analytic continuation into the half-space
it admits analytic continuation into the half-space  , in the sense that it admits a boundary-value representation
, in the sense that it admits a boundary-value representation  such that
such that 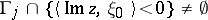 for every
for every 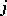 . This is equivalent to saying that near
. This is equivalent to saying that near 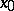 ,
,  , where
, where 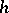 is the germ of a real-analytic function and
is the germ of a real-analytic function and 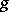 is a Fourier hyperfunction (cf. Hyperfunction) exponentially decreasing in a conic neighbourhood of
is a Fourier hyperfunction (cf. Hyperfunction) exponentially decreasing in a conic neighbourhood of 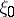 . The set of points
. The set of points  at which
at which 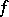 is not micro-analytic is called the singular spectrum of
is not micro-analytic is called the singular spectrum of 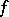 , and is denoted by
, and is denoted by 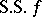 . By definition,
. By definition,
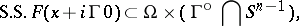
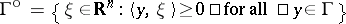 is the dual cone of
is the dual cone of 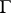 . Conversely, a hyperfunction satisfying this estimate can be written in the form
. Conversely, a hyperfunction satisfying this estimate can be written in the form 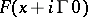 .
.
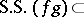
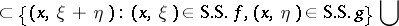

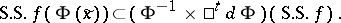
 does not appear in the
does not appear in the 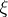 -component of the right-hand side. In particular, under coordinate transformation the singular spectrum behaves like a subset of
-component of the right-hand side. In particular, under coordinate transformation the singular spectrum behaves like a subset of  . Restriction
. Restriction  is possible if
is possible if 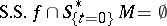 , in which case
, in which case  is said to contain
is said to contain 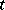 as real-analytic parameter at
as real-analytic parameter at 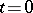 , and then
, and then
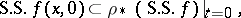
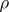 denotes projection on the
denotes projection on the 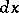 components. The dual assertion is:
components. The dual assertion is:
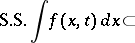
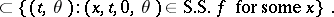

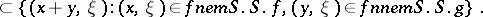
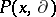 be a linear differential operator with real-analytic coefficients and let
be a linear differential operator with real-analytic coefficients and let 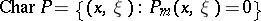 be its characteristic manifold. Then
be its characteristic manifold. Then
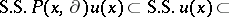
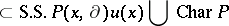
 ,
,  implies
implies 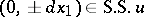 (the Kashiwara–Kawai Holmgren-type theorem); further, the fibre
(the Kashiwara–Kawai Holmgren-type theorem); further, the fibre  of
of 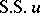 at
at  has the form
has the form  , where
, where 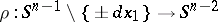 denotes projection to the equator
denotes projection to the equator 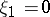 (the watermelon theorem).
(the watermelon theorem).
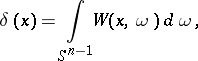
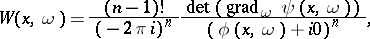
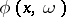 is a real-analytic function of
is a real-analytic function of 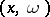 which is of positive type in
which is of positive type in  (that is,
(that is, 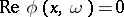 implies
implies 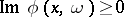 ), is homogeneous of degree 1 in
), is homogeneous of degree 1 in 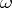 , and
, and 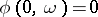 ,
, 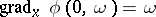 ; and the vector
; and the vector  is such that
is such that  . This is a generalization of the classical Radon decomposition, in which
. This is a generalization of the classical Radon decomposition, in which
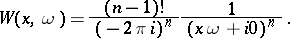
 , has a singular spectrum with only one direction
, has a singular spectrum with only one direction 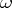 . Via convolution it gives a similar decomposition of general hyperfunctions. If
. Via convolution it gives a similar decomposition of general hyperfunctions. If  also satisfies
also satisfies 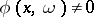 for
for 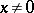 , then the singular spectrum of the component as a hyperfunction of
, then the singular spectrum of the component as a hyperfunction of  is precisely one point
is precisely one point 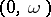 ; this is useful in applications. Typical examples are:
; this is useful in applications. Typical examples are:
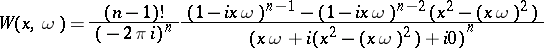
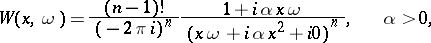
 is micro-analytic at
is micro-analytic at 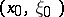 if and only if
if and only if 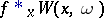 is real analytic in
is real analytic in 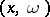 at
at 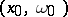 .
.
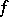 (the FBI-transform of
(the FBI-transform of 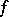 ) is
) is
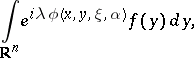
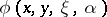 is a real-analytic function satisfying: 1) for
is a real-analytic function satisfying: 1) for 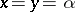 one has
one has 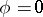 and
and 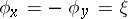 ; and 2)
; and 2)  for some
for some  . A typical example of such a
. A typical example of such a 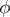 is
is
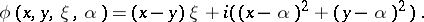
 is micro-analytic at
is micro-analytic at 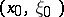 if and only if for some (equivalently, any) modification of
if and only if for some (equivalently, any) modification of  with compact support its FBI-transform is exponentially decreasing with respect to
with compact support its FBI-transform is exponentially decreasing with respect to  uniformly in
uniformly in 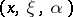 in a neighbourhood of
in a neighbourhood of 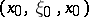 . Integration of the inversion formula over the radial variable gives the formula
. Integration of the inversion formula over the radial variable gives the formula
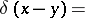
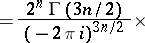
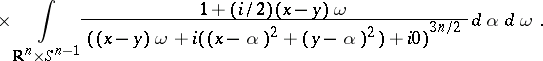
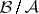 . All these arguments are compatible with the corresponding theory of (analytic) wave front sets for distributions.
. All these arguments are compatible with the corresponding theory of (analytic) wave front sets for distributions.
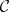 of micro-functions on
of micro-functions on 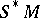 is the sheaf associated with the pre-sheaf
is the sheaf associated with the pre-sheaf
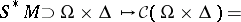
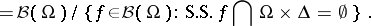
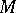 :
:
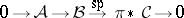
 denotes projection. By definition,
denotes projection. By definition,  for a hyperfunction
for a hyperfunction 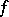 . The sheaf
. The sheaf  is flabby, which implies the possibility of arbitrary modification of hyperfunctions preserving the singular spectrum. Analytic pseudo-differential operators (cf. Pseudo-differential operator) and micro-differential operators naturally act on
is flabby, which implies the possibility of arbitrary modification of hyperfunctions preserving the singular spectrum. Analytic pseudo-differential operators (cf. Pseudo-differential operator) and micro-differential operators naturally act on 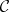 as sheaf homomorphisms. They act isomorphically at a non-characteristic point. Canonical transforms induce ring isomorphisms of the sheaf of pseudo-differential operators. Using these, a simple characteristic system of pseudo-differential equations can be locally reduced to the direct sum of copies of de Rham, Cauchy–Riemann and Lewy–Mizohata equations (the fundamental structure theorem).
as sheaf homomorphisms. They act isomorphically at a non-characteristic point. Canonical transforms induce ring isomorphisms of the sheaf of pseudo-differential operators. Using these, a simple characteristic system of pseudo-differential equations can be locally reduced to the direct sum of copies of de Rham, Cauchy–Riemann and Lewy–Mizohata equations (the fundamental structure theorem).
 is constructed from the sheaf
is constructed from the sheaf 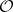 by Sato micro-localization: Let
by Sato micro-localization: Let 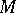 be a real-analytic manifold and
be a real-analytic manifold and 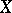 a complex neighbourhood of it. Let
a complex neighbourhood of it. Let 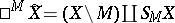 be the real blowing-up,
be the real blowing-up, 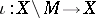 ,
, 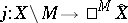 the canonical inclusions, and let
the canonical inclusions, and let 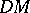 be the subset of the fibre product of
be the subset of the fibre product of 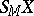 and
and 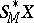 over
over 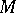 defined by
defined by  ; let
; let 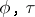 be the canonical projections to the factors. Let
be the canonical projections to the factors. Let  be the orientation sheaf of
be the orientation sheaf of  . Then
. Then