Micro-bundle
A mapping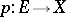 
which is a retraction (that is, there is a 
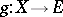for which 
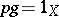) and which is locally trivial in the sense that for each 
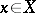there is a neighbourhood 
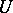of 
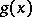in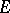 
which can be represented as a direct product 
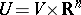, with 
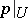the projection onto 
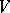. If for each such neighbourhood 
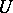there is fixed a piecewise-linear structure in each fibre 
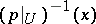, if, moreover, the projection of 
on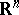 
is piecewise linear and for two neighbourhoods 
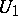and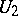 
and any 
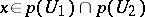the structures on 
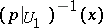and 
coincide in a neighbourhood of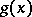 
, then the micro-bundle is called piecewise linear. Other structures may be introduced similarly.
The notion of a micro-bundle was introduced in order to define an analogue of the tangent bundle for a topological or piecewise-linear manifold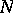 
. Namely, here 
, 
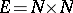and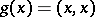 
. Each topological micro-bundle is equivalent to a unique locally trivial bundle with fibres 
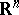of corresponding dimension, that is, there is a homeomorphism 
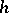of some neighbourhood 
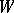of 
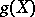in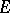 
into a neighbourhood 
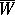of the zero section of some bundle 
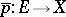with fibre 
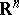. This fact is also true for piecewise-linear micro-bundles. Despite the fact that, because of this theorem, the notion of a micro-bundle has lost its theoretical interest, it is still used in concrete problems.
Comments
References
| [a1] | J. Milnor, "Microbundles, Part I" Topology , 3, Suppl. 1 (1964) pp. 53–80 |
| [a2] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) |
Micro-bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Micro-bundle&oldid=14340