Metric transitivity
of a dynamical system 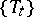 with a (quasi-) invariant measure
with a (quasi-) invariant measure 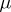
The property of 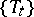 that any measurable subset
that any measurable subset 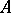 of the phase space
of the phase space 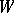 which is invariant relative to
which is invariant relative to 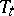 (in the sense that it coincides with its complete inverse images
(in the sense that it coincides with its complete inverse images 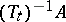 ) either has measure zero or coincides with
) either has measure zero or coincides with 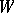 up to a set of measure zero. A formally stronger version of this property is obtained if in the definition instead of invariant sets one considers sets which are invariant modulo 0 (a set
up to a set of measure zero. A formally stronger version of this property is obtained if in the definition instead of invariant sets one considers sets which are invariant modulo 0 (a set 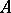 differing for each
differing for each 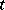 from
from  by a set of measure zero). These two versions are equivalent if
by a set of measure zero). These two versions are equivalent if 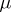 is a
is a 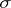 -finite measure and if the "time"
-finite measure and if the "time" 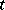 runs through a locally compact group with a countable base (see the proof for flows in [1]), but for arbitrary transformation groups this is not the case (see the example, given for another reason, in [2]).
runs through a locally compact group with a countable base (see the proof for flows in [1]), but for arbitrary transformation groups this is not the case (see the example, given for another reason, in [2]).
Instead of metric transitivity one may also speak of metric indecomposability, or ergodicity. If several (quasi-) invariant measures are considered in a given system and 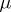 is one of them, then instead of speaking of metric transitivity (ergodicity) relative to
is one of them, then instead of speaking of metric transitivity (ergodicity) relative to 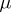 one speaks of metric transitivity (ergodicity) of
one speaks of metric transitivity (ergodicity) of 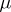 . Of course, decomposability of a normalized invariant measure
. Of course, decomposability of a normalized invariant measure 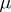 means something different, i.e. the possibility to represent
means something different, i.e. the possibility to represent 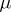 as
as 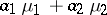 , where
, where  are normalized invariant measures different from
are normalized invariant measures different from 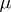 and
and 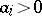 . Indecomposability of
. Indecomposability of 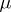 is equivalent to the second (stronger) version of metric transitivity (see [2], [3]).
is equivalent to the second (stronger) version of metric transitivity (see [2], [3]).
If there is a topology on 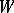 , then under natural assumptions (see the discussion for flows in [1]) metric transitivity implies that for almost-all
, then under natural assumptions (see the discussion for flows in [1]) metric transitivity implies that for almost-all 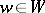 the trajectory of
the trajectory of 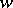 is everywhere dense (in this sense, metric transitivity implies topological transitivity). The converse is false.
is everywhere dense (in this sense, metric transitivity implies topological transitivity). The converse is false.
Starting with J. von Neumann , a number of results were obtained concerning the decomposition of non-ergodic systems into ergodic components. For the traditional, purely metric version (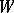 a Lebesgue space and only one (quasi-) invariant measure involved) see [5], [6], . N.M. Krylov and N.N. Bogolybov [7] obtained stronger results for topological flows and cascades on a metric compactum
a Lebesgue space and only one (quasi-) invariant measure involved) see [5], [6], . N.M. Krylov and N.N. Bogolybov [7] obtained stronger results for topological flows and cascades on a metric compactum 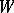 , of a twofold kind (see also [8], [9]): 1) a decomposition of normalized invariant measures, compatible with the topology, into ergodic measures; and 2) a "geometric" realization of all these decompositions at once by means of ergodic sets (cf. Ergodic set). Regarding the generalization of these results to other transformation groups, it is known that 1) is valid under broader assumptions than 2) (see [2], [3]). There are also similar results for dynamical systems (at present only cascades and flows) in appropriate measurable spaces (cf. Measurable space) and (or) for quasi-invariant measures (see [9]–[10]).
, of a twofold kind (see also [8], [9]): 1) a decomposition of normalized invariant measures, compatible with the topology, into ergodic measures; and 2) a "geometric" realization of all these decompositions at once by means of ergodic sets (cf. Ergodic set). Regarding the generalization of these results to other transformation groups, it is known that 1) is valid under broader assumptions than 2) (see [2], [3]). There are also similar results for dynamical systems (at present only cascades and flows) in appropriate measurable spaces (cf. Measurable space) and (or) for quasi-invariant measures (see [9]–[10]).
Metric transitivity of a partition 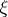 of a measure space
of a measure space 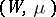 is the property that any measurable subset
is the property that any measurable subset 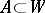 consisting entirely of elements of
consisting entirely of elements of 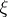 either has measure zero or coincides with
either has measure zero or coincides with 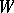 up to a set of measure zero. Instead of metric transitivity one also speaks of absolute non-measurability of
up to a set of measure zero. Instead of metric transitivity one also speaks of absolute non-measurability of 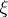 . Metric transitivity of a dynamical system generated by a group of transformations, whose trajectories form a partition of the phase space, coincides with metric transitivity of this partition. If the transformations forming the dynamical system are not invertible, then their metric transitivity also reduces to that of some partition; however, its description is more complicated: the element containing some point consists of all images of the point and all inverse images of these images.
. Metric transitivity of a dynamical system generated by a group of transformations, whose trajectories form a partition of the phase space, coincides with metric transitivity of this partition. If the transformations forming the dynamical system are not invertible, then their metric transitivity also reduces to that of some partition; however, its description is more complicated: the element containing some point consists of all images of the point and all inverse images of these images.
References
| [1] | E. Hopf, "Ergodentheorie" , Springer (1937) |
| [2] | S.V. Fomin, "On measures invariant under certain groups of transformations" Izv. Akad. Nauk SSSR Ser. Mat. , 14 : 3 (1950) pp. 261–274 (In Russian) |
| [3] | N.N. Bogolyubov, "On some ergodic properties of continuous transformation groups" , Selected Works , 1 , Kiev (1969) pp. 561–569 (In Russian) |
| [4a] | J. von Neumann, "Zur Operatorenmethode in der klassischen Mechanik" Ann. of Math. , 33 : 3 (1932) pp. 587–642 |
| [4b] | J. von Neumann, "Zusätze zur Arbeit "Zur Operatorenmethode in der klassischen Mechanik" " Ann. of Math. , 33 : 4 (1933) pp. 789–792 |
| [5] | V.A. Rokhlin, "Selected topics from the metric theory of dynamical systems" Transl. Amer. Math. Soc. Ser. 2 , 49 (1966) pp. 171–240 Uspekhi Mat. Nauk , 4 : 2 (1949) pp. 57–128 |
| [6] | V.A. Rokhlin, "On the decomposition of a dynamical system into transitive components" Mat. Sb. , 25 : 2 (1949) pp. 235–249 (In Russian) |
| [7] | N.N. Bogolyubov, N.M. Krylov, "La theorie générale de la mesure dans son application à l'étude des systèmes dynamiques de la mécanique non-linéaire" Ann. of Math. (2) , 38 (1937) pp. 65–113 |
| [8] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [9] | J. Oxtoby, "Ergodic sets" Bull. Amer. Math. Soc. , 58 (1952) pp. 116–136 |
| [10] | Yu.I. Kifer, S.A. Pirogov, "The decomposition of quasi-ergodic measures into ergodic components" Uspekhi Mat. Nauk , 27 : 5 (1972) pp. 239–240 (In Russian) |
Comments
The term "ergodic" is mostly used for the first version of metric transitivity; for the second (stranger) version sometimes the term "irreducible" is used; see e.g. [a4]. The two notions coincide if for every measurable subset  of
of 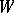 which is invariant
which is invariant 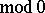 there exists an invariant measurable subset
there exists an invariant measurable subset 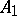 of
of 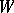 such that
such that  . For conditions such that this holds, see also (the proof of) Lemma 1 in Chapt. 1, § 2 of [a8], and e.g. Lemma 3.3 in [a6]. A simple example where the two notions do not coincide is in [a5], p. 84.
. For conditions such that this holds, see also (the proof of) Lemma 1 in Chapt. 1, § 2 of [a8], and e.g. Lemma 3.3 in [a6]. A simple example where the two notions do not coincide is in [a5], p. 84.
What is called above "indecomposability" is usually expressed by saying that 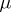 is an extreme point of the (convex) set
is an extreme point of the (convex) set 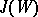 of all invariant probability measures on
of all invariant probability measures on 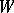 (a probability measure is a normalized measure). Proofs of the fact that an invariant probability measure is indecomposable (i.e., is an extreme point of
(a probability measure is a normalized measure). Proofs of the fact that an invariant probability measure is indecomposable (i.e., is an extreme point of 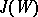 ) if and only if it is irreducible (according to the above definition), under various conditions for
) if and only if it is irreducible (according to the above definition), under various conditions for 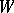 or
or 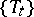 , can also be found in [a1] and in [a6]; also the proof of theorem 6.10(iii) in [a7] can easily be adapted to the case of a general semi-group
, can also be found in [a1] and in [a6]; also the proof of theorem 6.10(iii) in [a7] can easily be adapted to the case of a general semi-group 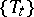 and arbitrary
and arbitrary 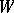 .
.
As to the decomposition of the phase space into ergodic components, see also [a6] and [a2]. Such decompositions lead to representations of invariant measures as integrals of ergodic measures; if the phase space 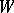 is compact, this is an easy consequence of Choquet theory: see [a5], p. 82. For such a representation in the context of random transformations, see Appendix A.1 in [a3].
is compact, this is an easy consequence of Choquet theory: see [a5], p. 82. For such a representation in the context of random transformations, see Appendix A.1 in [a3].
References
| [a1] | J.R. Blum, D.L. Hanson, "On invariant probability measures I" Pacific J. Math. , 10 (1960) pp. 1125–1129 |
| [a2] | R.H. Farrell, "Representation of invariant measures" Illinois J. Math. , 6 (1962) pp. 447–467 |
| [a3] | Y. Kifer, "Ergodic theory of random transformations" , Birkhäuser (1986) |
| [a4] | G.W. Mackey, "Point realizations of transformation groups" Illinois J. Math. , 6 (1962) pp. 327–335 |
| [a5] | R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966) |
| [a6] | V.S. Varadarajan, "Groups of automorphisms of Borel spaces" Trans. Amer. Math. Soc. , 109 (1963) pp. 191–220 |
| [a7] | P. Walters, "An introduction to ergodic theory" , Springer (1982) |
| [a8] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
Metric transitivity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric_transitivity&oldid=17732