Difference between revisions of "Metric projection"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | m0636701.png | ||
| + | $#A+1 = 19 n = 1 | ||
| + | $#C+1 = 19 : ~/encyclopedia/old_files/data/M063/M.0603670 Metric projection, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''operator of best approximation'' | ''operator of best approximation'' | ||
| − | A many-valued mapping | + | A many-valued mapping $ P _ {M} : x \rightarrow P _ {M} x $, |
| + | associating to each element $ x $ | ||
| + | of a metric space $ X = ( X , \rho ) $ | ||
| + | the set | ||
| − | + | $$ | |
| + | P _ {M} x = \ | ||
| + | \{ {m \in M } : {\rho ( x , m ) = \rho ( x , M ) } \} | ||
| + | $$ | ||
| − | of elements of best approximation (cf. [[Element of best approximation|Element of best approximation]]) from the set | + | of elements of best approximation (cf. [[Element of best approximation|Element of best approximation]]) from the set $ M \subset X $. |
| + | If $ M $ | ||
| + | is a [[Chebyshev set|Chebyshev set]], then the metric projection is a single-valued mapping. The problem of constructing an element of best approximation is often solved approximately, that is, an element is determined in the set | ||
| − | + | $$ | |
| + | P _ {M} ^ {t} x = \ | ||
| + | \{ {m \in M } : {\rho ( x , m ) \leq t + \rho ( x , M ) } \} | ||
| + | , | ||
| + | $$ | ||
| − | where | + | where $ t > 0 $ |
| + | is sufficiently small. From the properties of the mapping $ P _ {M} ^ {t} : x \rightarrow P _ {M} ^ {t} x $ | ||
| + | it is sometimes possible to obtain properties of the set $ M $. | ||
| + | E.g., if for any element $ x $ | ||
| + | of a normed space $ X $ | ||
| + | a number $ t = t ( x) > 0 $ | ||
| + | exists such that $ P _ {M} ^ {t} x $ | ||
| + | is convex (connected), then $ M $ | ||
| + | is convex (respectively, connected). | ||
| − | From the point of view of applications it is useful to know whether the metric projection has such properties as linearity, continuity, uniform continuity, etc. A metric projection on a Chebyshev subspace of a normed space is, in general, not linear. If the metric projection on each subspace of fixed dimension is single-valued and linear, then | + | From the point of view of applications it is useful to know whether the metric projection has such properties as linearity, continuity, uniform continuity, etc. A metric projection on a Chebyshev subspace of a normed space is, in general, not linear. If the metric projection on each subspace of fixed dimension is single-valued and linear, then $ X $ |
| + | is linearly isometric to an inner-product space. The metric projection on a non-empty [[Approximately-compact set|approximately-compact set]] in a metric space is upper semi-continuous; in particular, in a normed space the metric projection onto a finite-dimensional Chebyshev subspace is continuous; the metric projection may be not lower semi-continuous if the subspace is not Chebyshev. There exists a reflexive strictly-convex space and an infinite-dimensional subspace on which the metric projection is discontinuous. The metric projection on any closed convex set $ M $ | ||
| + | in a Hilbert space satisfies a Lipschitz condition: | ||
| − | + | $$ | |
| + | \| P _ {M} x - P _ {M} y \| \leq K \| x - y \| , | ||
| + | $$ | ||
| − | with constant | + | with constant $ K = 1 $. |
The continuity property of a metric projection and its generalizations have found applications in ill-posed problems, in the convexity problem for Chebyshev sets, in the construction of elements of best approximation, etc. | The continuity property of a metric projection and its generalizations have found applications in ill-posed problems, in the convexity problem for Chebyshev sets, in the construction of elements of best approximation, etc. | ||
Latest revision as of 08:00, 6 June 2020
operator of best approximation
A many-valued mapping $ P _ {M} : x \rightarrow P _ {M} x $, associating to each element $ x $ of a metric space $ X = ( X , \rho ) $ the set
$$ P _ {M} x = \ \{ {m \in M } : {\rho ( x , m ) = \rho ( x , M ) } \} $$
of elements of best approximation (cf. Element of best approximation) from the set $ M \subset X $. If $ M $ is a Chebyshev set, then the metric projection is a single-valued mapping. The problem of constructing an element of best approximation is often solved approximately, that is, an element is determined in the set
$$ P _ {M} ^ {t} x = \ \{ {m \in M } : {\rho ( x , m ) \leq t + \rho ( x , M ) } \} , $$
where $ t > 0 $ is sufficiently small. From the properties of the mapping $ P _ {M} ^ {t} : x \rightarrow P _ {M} ^ {t} x $ it is sometimes possible to obtain properties of the set $ M $. E.g., if for any element $ x $ of a normed space $ X $ a number $ t = t ( x) > 0 $ exists such that $ P _ {M} ^ {t} x $ is convex (connected), then $ M $ is convex (respectively, connected).
From the point of view of applications it is useful to know whether the metric projection has such properties as linearity, continuity, uniform continuity, etc. A metric projection on a Chebyshev subspace of a normed space is, in general, not linear. If the metric projection on each subspace of fixed dimension is single-valued and linear, then $ X $ is linearly isometric to an inner-product space. The metric projection on a non-empty approximately-compact set in a metric space is upper semi-continuous; in particular, in a normed space the metric projection onto a finite-dimensional Chebyshev subspace is continuous; the metric projection may be not lower semi-continuous if the subspace is not Chebyshev. There exists a reflexive strictly-convex space and an infinite-dimensional subspace on which the metric projection is discontinuous. The metric projection on any closed convex set $ M $ in a Hilbert space satisfies a Lipschitz condition:
$$ \| P _ {M} x - P _ {M} y \| \leq K \| x - y \| , $$
with constant $ K = 1 $.
The continuity property of a metric projection and its generalizations have found applications in ill-posed problems, in the convexity problem for Chebyshev sets, in the construction of elements of best approximation, etc.
References
| [1] | I.M. Singer, "The theory of best approximation and functional analysis" , CBMS Regional Conf. Ser. , 13 , SIAM (1974) |
| [2] | L.P. Vlasov, "Approximative properties of sets in normed linear spaces" Russian Math. Surveys , 28 : 6 (1973) pp. 3–66 Uspekhi Mat. Nauk , 28 : 6 (1973) pp. 3–66 |
| [3] | V.I. Berdyshev, "Uniform continuity of the metric projection and of the 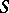 -projection" , Theory of Approximation of Functions. Internat. Conf., Kaluga 1975 , Moscow (1977) pp. 37–41 (In Russian) -projection" , Theory of Approximation of Functions. Internat. Conf., Kaluga 1975 , Moscow (1977) pp. 37–41 (In Russian) |
Metric projection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric_projection&oldid=13496