Mersenne number
A prime number of the form  , where
, where 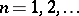 . Mersenne numbers were considered in the 17th century by M. Mersenne. The numbers
. Mersenne numbers were considered in the 17th century by M. Mersenne. The numbers  can be prime only for prime values of
can be prime only for prime values of  . For
. For  one obtains the prime numbers
one obtains the prime numbers  . However, for
. However, for  the number
the number 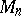 is composite. For prime values of
is composite. For prime values of  larger than
larger than 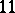 , among the
, among the  one encounters both prime and composite numbers. The fast growth of the numbers
one encounters both prime and composite numbers. The fast growth of the numbers 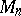 makes their study difficult. By considering concrete numbers
makes their study difficult. By considering concrete numbers 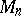 it has been shown, for example, that
it has been shown, for example, that 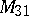 (L. Euler, 1750) and
(L. Euler, 1750) and  (I.M. Pervushin, 1883) are Mersenne numbers. Computers were used to find other very large Mersenne numbers, among them
(I.M. Pervushin, 1883) are Mersenne numbers. Computers were used to find other very large Mersenne numbers, among them 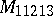 . The existence of an infinite set of Mersenne numbers is still an open problem (1989). This problem is closely related with the problem on the existence of perfect numbers.
. The existence of an infinite set of Mersenne numbers is still an open problem (1989). This problem is closely related with the problem on the existence of perfect numbers.
References
| [1] | H. Hasse, "Vorlesungen über Zahlentheorie" , Springer (1950) |
| [2] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
Comments
Presently (1989) it is known that for the following  the Mersenne number
the Mersenne number  is prime: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 132049, 216091. See [a1].
is prime: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 132049, 216091. See [a1].
The Lucas test provides a very simple method to establish primality of these numbers. This test consists of the following (cf. [a2]). Define  and
and 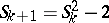 for
for  . Then
. Then 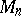 is prime if and only if
is prime if and only if 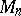 divides
divides 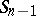 (and
(and  is a prime number).
is a prime number).
References
| [a1] | H. Riesel, "Prime numbers and computer methods for factorisation" , Birkhäuser (1986) |
| [a2] | D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978) |
Mersenne number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mersenne_number&oldid=12973