Mergelyan theorem

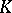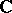A theorem on the possibility of uniform approximation of functions of one complex variable by polynomials. Let be a compact subset of the complex -plane with a connected complement. Then every function 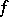continuous on 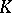and holomorphic at its interior points can be approximated uniformly on 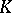by polynomials in .

This theorem was proved by S.N. Mergelyan (see [1], [2]); it is the culmination of a large number of studies on approximation theory in the complex plane and has many applications in various branches of complex analysis.

In the case where 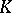has no interior points this result was proved by M.A. Lavrent'ev [3]; the corresponding theorem in the case where 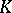is a compact domain with a connected complement is due to M.V. Keldysh [4] (cf. also Keldysh–Lavrent'ev theorem).

Mergelyan's theorem has the following consequence. Let 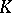be an arbitrary compact subset of 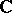. Let a function 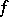be continuous on 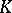and holomorphic in its interior. Then in order that 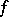be uniformly approximable by polynomials in it is necessary and sufficient that 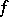admits a holomorphic extension to all bounded connected components of the set .

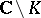The problem of polynomial approximation is a particular case of the problem of approximation by rational functions with poles in the complement of 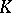. Mergelyan found also several sufficient conditions for rational approximation (see [2]). A complete solution of this problem (for compacta 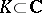) was obtained in terms of analytic capacities (cf. Analytic capacity), [5].

Mergelyan's theorem touches upon a large number of papers concerning polynomial, rational and holomorphic approximation in the space 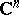of several complex variables. Here only partial results for special types of compact subsets have been obtained up till now.

References

[1]	S.N. Mergelyan, "On the representation of functions by series of polynomials on closed sets" Transl. Amer. Math. Soc. , 3 (1962) pp. 287–293 Dokl. Akad. Nauk SSSR , 78 : 3 (1951) pp. 405–408
[2]	S.N. Mergelyan, "Uniform approximation to functions of a complex variable" Transl. Amer. Math. Soc. , 3 (1962) pp. 294–391 Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 31–122
[3]	M.A. [M.A. Lavrent'ev] Lavrentieff, "Sur les fonctions d'une variable complexe représentables par des series de polynômes" , Hermann (1936)
[4]	M.V. Keldysh, "Sur la réprésentation par des séries de polynômes des fonctions d'une variable complexe dans des domaines fermés" Mat. Sb. , 16 : 3 (1945) pp. 249–258
[5]	A.G. Vitushkin, "The analytic capacity of sets in problems of approximation theory" Russian Math. Surveys , 22 : 6 (1967) pp. 139–200 Uspekhi Mat. Nauk , 22 : 6 (1967) pp. 141–199
[6]	, Some questions in approximation theory , Moscow (1963) (In Russian; translated from English)
[7]	T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969)

Comments

Another important forerunner of Mergelyan's theorem was the Walsh theorem: the case where 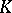is the closure of a Jordan domain (a set with boundary consisting of Jordan curves, cf. Jordan curve).

An interesting proof of Mergelyan's theorem, based on functional analysis, is due to L. Carlesson, see [a1].

For analogues of Mergelyan's theorem in 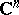, see [a2]. See also Approximation of functions of a complex variable.

References

[a1]	L. Carlesson, "Mergelyan's theorem on uniform polynomial approximation" Math. Scand. , 15 (1964) pp. 167–175
[a2]	E.M. Chirka, G.M. Khenkin, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 : 5 (1976) pp. 612–687 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142
[a3]	D. Gaier, "Lectures on complex approximation" , Birkhäuser (1987) (Translated from German)